三角関数の公式は多岐にわたり、覚えるのが大変と感じる方も多いでしょう。しかし、安心してください。実際にはすべての公式を暗記する必要はありません。三角関数の定義や加法定理を理解すれば、多くの公式は自然と導き出せるのです。
本記事では、まず三角関数の定義と加法定理について詳しく解説し、それらを基にして他の公式を導出します。また、公式同士の関連性も整理しながら、単なる丸暗記ではなく、理解を深めることで自然に覚えることができる方法を紹介します。
本記事では以下のように三角関数の公式を分類していますので、参考にしてください。
(1)三角関数の定義を使って証明されるグループ
(2)加法定理を使って証明されるグループ
三角関数の定義
三角関数にはサイン(sin)、コサイン(cos)、タンジェント(tan)の3つがあります。これらはそもそもは直角三角形における辺の比率です。しかし直角三角形という前提があると角の大きさとして鋭角(0 ∘ 0^\circ 0 ∘ 9 0 ∘ 90^\circ 9 0 ∘
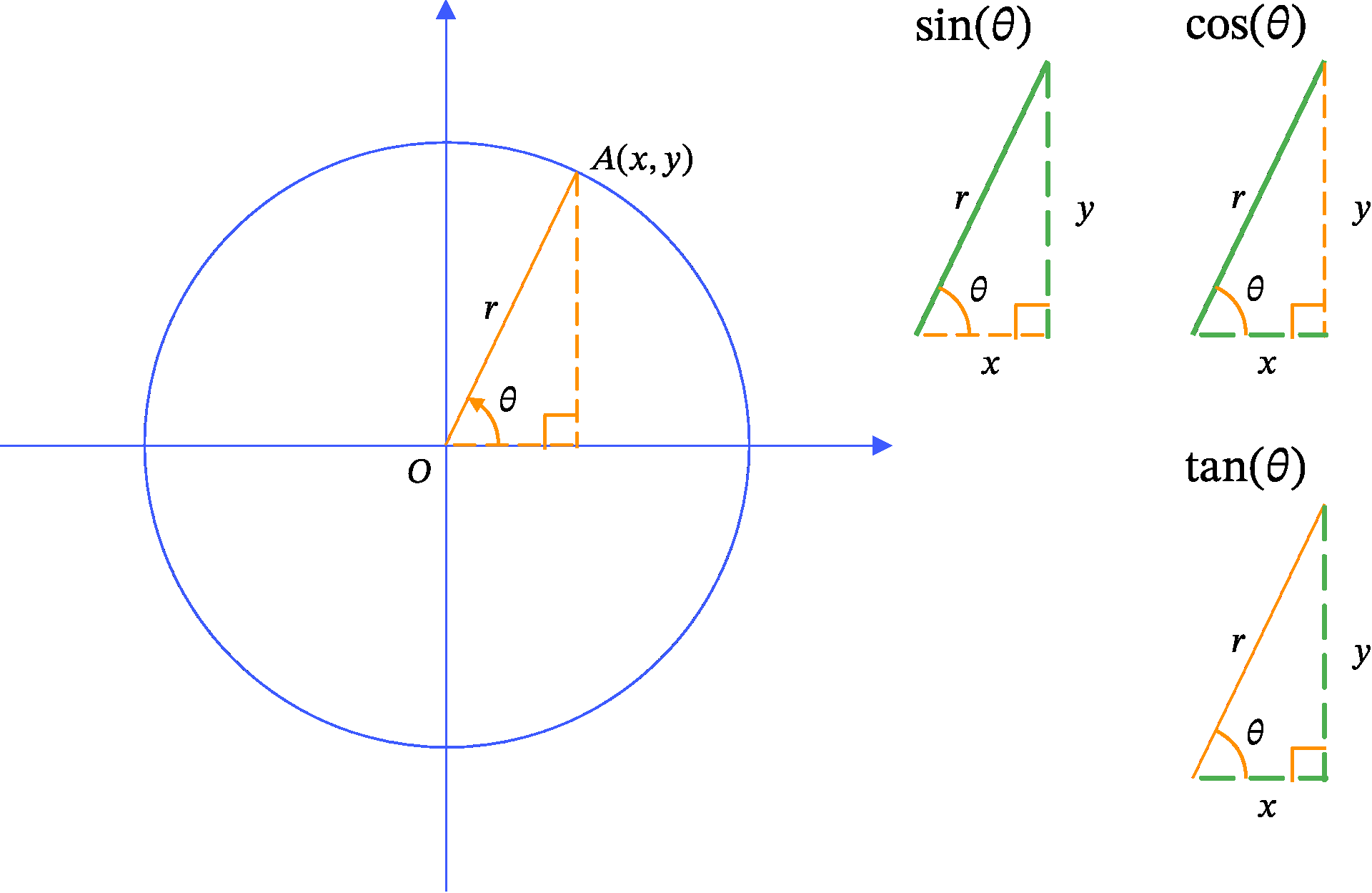
まずは Figure 1 を見て三角関数の定義を確認してください。
Figure 1 では以下のステップで円や点を作成しています。
中心が原点 O O O r r r
この円周上に適当に点 A A A A A A ( x , y ) (x, y) ( x , y )
点 A A A O A OA O A
x x x O A OA O A θ \theta θ θ \theta θ x x x
この r r r x x x y y y θ \theta θ
sin ( θ ) = y r \sin(\theta) = \frac{y}{r} sin ( θ ) = r y cos ( θ ) = x r \cos(\theta) = \frac{x}{r} cos ( θ ) = r x tan ( θ ) = y x \tan(\theta) = \frac{y}{x} tan ( θ ) = x y
これらの基本的な定義を理解することが、後続する内容への基盤となります。
加法定理
加法定理は、異なる角度を持つ三角関数を結びつけるための重要なツールです。具体的には以下のようになります:
角度が A − B A-B A − B Theorem 1 において B B B − B -B − B
加法定理は三角関数の定義と並んで、他の公式を導くための基盤になります。加法定理自体は覚えておきましょう。
三角関数の等式の体系的な整理
三角関数には多くの公式が存在し、それらを体系的に整理することが大切です。最初に述べた通り、これらの公式は三角関数の定義と加法定理を用いて簡単に導出できます。本記事では三角関数の公式を整理した後、いくつか公式をピックアップして、実際に導出できることをご紹介します。
定義から導出する公式
これらの公式は三角関数の定義から求めることができます。
sin 2 θ + cos 2 θ = 1 (1)
\sin^2{\theta} + \cos^2{\theta} = 1
\tag{1} sin 2 θ + cos 2 θ = 1 ( 1 )
tan ( θ ) = sin θ cos θ (2)
\tan(\theta) = \frac{\sin{\theta}}{\cos{\theta}}
\tag{2} tan ( θ ) = cos θ sin θ ( 2 )
1 + tan 2 θ = 1 cos 2 θ (3)
1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}}
\tag{3} 1 + tan 2 θ = cos 2 θ 1 ( 3 )
sin ( − θ ) = − sin θ (4)
\sin{(-\theta)} = -\sin{\theta}
\tag{4} sin ( − θ ) = − sin θ ( 4 )
cos ( − θ ) = cos θ (5)
\cos{(-\theta)} = \cos{\theta}
\tag{5} cos ( − θ ) = cos θ ( 5 )
tan ( − θ ) = − tan θ (6)
\tan{(-\theta)} = -\tan{\theta}
\tag{6} tan ( − θ ) = − tan θ ( 6 )
sin ( π − θ ) = sin θ (7)
\sin{(\pi - \theta)} = \sin{\theta}
\tag{7} sin ( π − θ ) = sin θ ( 7 )
cos ( π − θ ) = − cos θ (8)
\cos{(\pi - \theta)} = -\cos{\theta}
\tag{8} cos ( π − θ ) = − cos θ ( 8 )
tan ( π − θ ) = − tan θ (9)
\tan{(\pi - \theta)} = -\tan{\theta}
\tag{9} tan ( π − θ ) = − tan θ ( 9 )
sin ( π 2 − θ ) = cos θ (10)
\sin{\left(\frac{\pi}{2} - \theta \right)} = \cos{\theta}
\tag{10} sin ( 2 π − θ ) = cos θ ( 10 )
cos ( π 2 − θ ) = sin θ (11)
\cos{\left(\frac{\pi}{2} - \theta \right)} = \sin{\theta}
\tag{11} cos ( 2 π − θ ) = sin θ ( 11 )
tan ( π 2 − θ ) = 1 tan θ (12)
\tan{\left(\frac{\pi}{2} - \theta \right)} = \frac{1}{\tan{\theta}}
\tag{12} tan ( 2 π − θ ) = tan θ 1 ( 12 )
加法定理から導出する公式
これらの公式は加法定理を使って求めることができます。
2倍角の公式
sin 2 θ = 2 sin θ cos θ (13)
\sin{2\theta} = 2\sin\theta\cos\theta
\tag{13} sin 2 θ = 2 sin θ cos θ ( 13 )
cos 2 θ = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ (14)
\cos{2\theta} = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2\sin^2\theta
\tag{14} cos 2 θ = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ ( 14 )
tan 2 θ = 2 tan θ 1 − tan 2 θ ( 1 − tan 2 θ ≠ 0 ) (15)
\tan{2\theta} = \frac{2\tan\theta}{1 - \tan^2\theta} \quad (1 - \tan^2θ \neq 0)
\tag{15} tan 2 θ = 1 − tan 2 θ 2 tan θ ( 1 − tan 2 θ = 0 ) ( 15 )
半角の公式
sin 2 α 2 = 1 − cos α 2 (16)
\sin ^{2}\dfrac{\alpha }{2}=\frac{1 - \cos \alpha }{2}
\tag{16} sin 2 2 α = 2 1 − cos α ( 16 )
cos 2 α 2 = 1 + cos α 2 (17)
\cos ^{2}\dfrac{\alpha }{2}=\dfrac{1+\cos \alpha }{2}
\tag{17} cos 2 2 α = 2 1 + cos α ( 17 )
tan 2 α 2 = 1 − cos α 1 + cos α (18)
\tan ^{2}\dfrac{\alpha }{2}=\dfrac{1-\cos \alpha }{1+\cos \alpha }
\tag{18} tan 2 2 α = 1 + cos α 1 − cos α ( 18 )
三角関数の合成
a sin θ + b cos θ = a 2 + b 2 sin ( θ + α ) (19)
a\sin \theta + b\cos \theta =\sqrt{a^{2}+b^{2}} \sin \left( \theta +\alpha \right)
\tag{19} a sin θ + b cos θ = a 2 + b 2 sin ( θ + α ) ( 19 )
ここで、
cos α = a a 2 + b 2 , sin α = b a 2 + b 2 .
\begin{aligned}
\cos \alpha &= \dfrac{a}{\sqrt{a^{2}+b^{2}}},\\
\sin \alpha &= \dfrac{b}{\sqrt{a^{2}+b^{2}}}.
\end{aligned}
cos α sin α = a 2 + b 2 a , = a 2 + b 2 b .
公式の導出
ここまでご紹介した以外にも三角関数の公式は多くあります。全て丸暗記することは大変ですし、何より数学的な理解につながりません。ある公式が何から導出できるかを理解しておくと、公式間のつながりがわかり、ストーリーが生まれます。ストーリーをベースにして公式を分類・理解することで、単なる丸暗記ではない、理解と応用力を伴った暗記 を行いましょう。
ここでは上記の公式からいくつかピックアップして確かにそれらの公式が定義や加法定理から導かれることを確認します。なお厳密な証明は目的ではなく、あくまでも公式間の関係について理解を深めることを目的としています。
定義を使った導出
sin 2 θ + cos 2 θ = 1 \sin^2{\theta} + \cos^2{\theta} = 1 sin 2 θ + cos 2 θ = 1
三角関数は円を使って定義されます。円は1点(中心)からの距離(r r r Figure 1 中にある円周上の任意の点である、点 A A A x x x y y y
x 2 + y 2 = r 2 (20)
x^2 + y^2 = r^2
\tag{20} x 2 + y 2 = r 2 ( 20 )
ところで三角関数の定義を見ると、sin θ \sin \theta sin θ y y y cos θ \cos \theta cos θ x x x x 2 + y 2 x^2 + y^2 x 2 + y 2 Equation 20 を使えそうです。
ということで、試しに sin θ \sin \theta sin θ cos θ \cos \theta cos θ
sin 2 θ + cos 2 θ = ( y r ) 2 + ( x r ) 2 = y 2 r 2 + x 2 r 2 = x 2 + y 2 r 2 = r 2 r 2 ( ∵ x 2 + y 2 = r 2 ) = 1.
\begin{aligned}
\sin ^{2}\theta +\cos ^{2}\theta &= \left( \dfrac{y}{r}\right) ^{2}+\left( \dfrac{x}{r}\right) ^{2}\\
&=\dfrac{y^{2}}{r^{2}}+\dfrac{x^{2}}{r^{2}}\\
&=\dfrac{x^{2}+y^{2}}{r^{2}}\\
&=\dfrac{r^{2}}{r^{2}} \qquad \left( \because x^{2}+y^{2}=r^{2}\right) \\
&=1.
\end{aligned}
sin 2 θ + cos 2 θ = ( r y ) 2 + ( r x ) 2 = r 2 y 2 + r 2 x 2 = r 2 x 2 + y 2 = r 2 r 2 ( ∵ x 2 + y 2 = r 2 ) = 1.
確かに Equation 1 が導かれました。定義からあっさりと導けたと思います。実質的に、中心と円周上の点の距離は半径であることを述べている式であるといえるでしょう。
1 + tan 2 θ = 1 cos 2 θ 1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}} 1 + tan 2 θ = c o s 2 θ 1
Equation 1 は sin θ \sin \theta sin θ cos θ \cos \theta cos θ cos θ \cos \theta cos θ tan θ \tan \theta tan θ Equation 1 の両辺を sin 2 θ \sin ^2 \theta sin 2 θ sin 2 θ \sin^2 \theta sin 2 θ sin θ \sin \theta sin θ cos 2 θ \cos ^2 \theta cos 2 θ cos θ = 0 \cos \theta = 0 cos θ = 0
sin 2 θ + cos 2 θ = 1 sin 2 θ cos 2 θ + cos 2 θ cos 2 θ = 1 cos 2 θ sin 2 θ cos 2 θ + 1 = 1 cos 2 θ . (21)
\begin{aligned}
\sin ^2 \theta + \cos ^2 \theta &= 1 \\
\frac{\sin ^2 \theta}{\cos ^2 \theta} + \frac{\cos ^2 \theta}{\cos ^2 \theta} &= \frac{1}{\cos ^2 \theta} \\
\frac{\sin ^2 \theta}{\cos ^2 \theta} + 1 &= \frac{1}{\cos ^2 \theta}.
\end{aligned}
\tag{21} sin 2 θ + cos 2 θ cos 2 θ sin 2 θ + cos 2 θ cos 2 θ cos 2 θ sin 2 θ + 1 = 1 = cos 2 θ 1 = cos 2 θ 1 . ( 21 )
cos 2 θ cos 2 θ = 1 \frac{\cos ^2 \theta}{\cos ^2 \theta} = 1 c o s 2 θ c o s 2 θ = 1 Equation 2 に似ていませんか?Equation 2 より、
sin 2 θ cos 2 θ = ( sin θ cos θ ) 2 = tan 2 θ
\frac{\sin ^2 \theta}{\cos ^2 \theta} = \left( \frac{\sin \theta}{\cos \theta} \right)^2
= \tan^2 \theta
cos 2 θ sin 2 θ = ( cos θ sin θ ) 2 = tan 2 θ
ですから、tan θ \tan \theta tan θ sin θ \sin \theta sin θ Equation 21 は以下のようになります。
sin 2 θ cos 2 θ + 1 = 1 cos 2 θ tan 2 θ + 1 = 1 cos 2 θ
\begin{aligned}
\frac{\sin ^2 \theta}{\cos ^2 \theta} + 1 &= \frac{1}{\cos ^2 \theta} \\
\tan ^2 \theta + 1 &= \frac{1}{\cos ^2 \theta}
\end{aligned}
cos 2 θ sin 2 θ + 1 tan 2 θ + 1 = cos 2 θ 1 = cos 2 θ 1
無事に Equation 3 を導出できました。
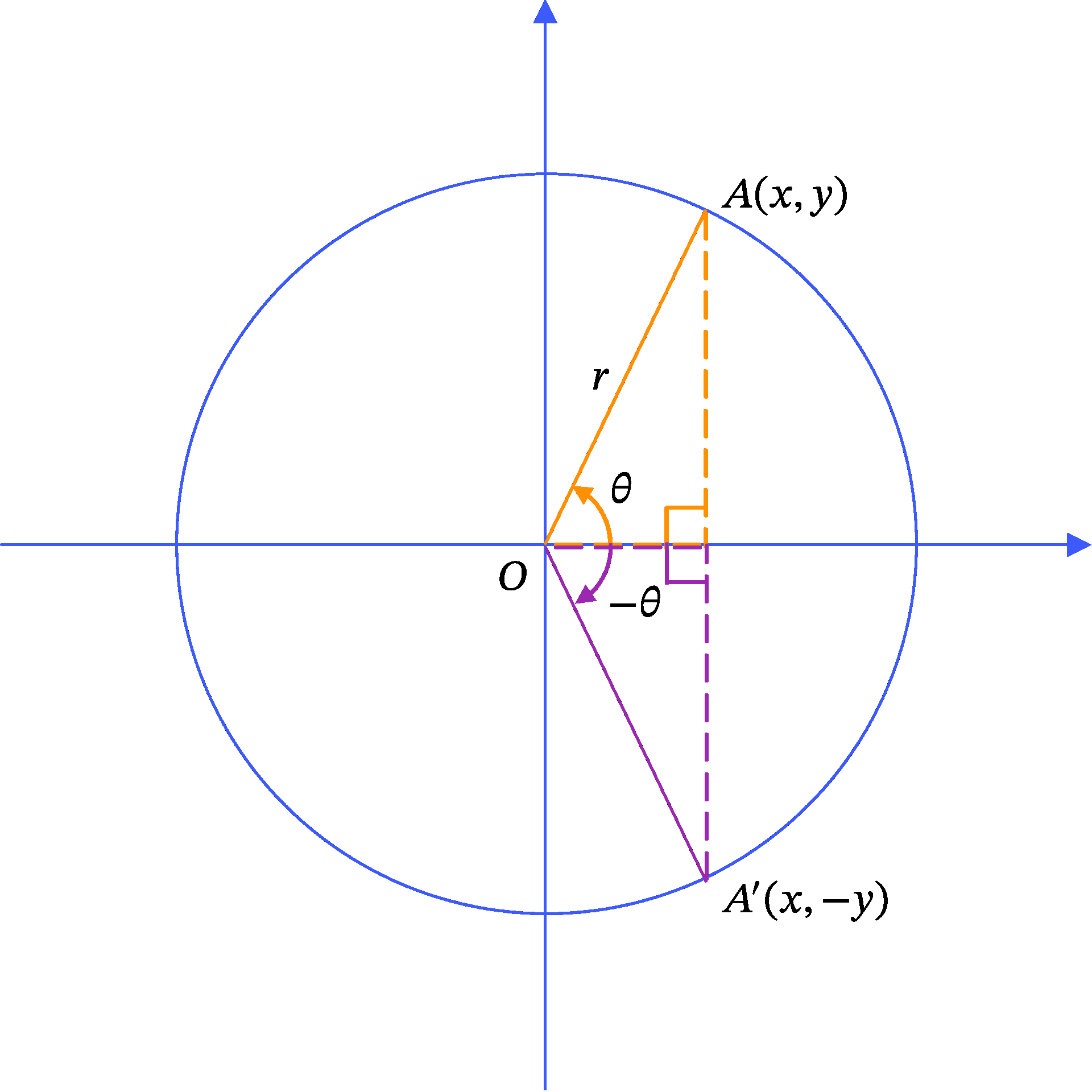
sin ( − θ ) = − sin θ \sin{(-\theta)} = -\sin{\theta} sin ( − θ ) = − sin θ cos ( − θ ) = cos θ \cos{(-\theta)} = \cos{\theta} cos ( − θ ) = cos θ
このタイプの公式では、 θ \theta θ A A A − θ - \theta − θ A ′ A' A ′ Figure 2 )。
三角関数の定義を使うと sin ( − θ ) \sin (-\theta) sin ( − θ ) A ′ ( x , − y ) A'(x, -y) A ′ ( x , − y )
sin ( − θ ) = − y r = − y r = − sin θ .
\begin{aligned}
\sin (-\theta) &= \frac{-y}{r} \\
&= - \frac{y}{r} \\
&= - \sin \theta.
\end{aligned}
sin ( − θ ) = r − y = − r y = − sin θ .
円を使った三角関数の定義を使うと、簡単に導き出せますね?
もう一つ、 cos ( − θ ) = cos θ \cos{(-\theta)} = \cos{\theta} cos ( − θ ) = cos θ
先ほどと同様に考えますが、コサインの計算ですので今度は x x x
cos ( − θ ) = x r = cos θ .
\begin{aligned}
\cos (-\theta) &= \frac{x}{r} \\
&= \cos \theta.
\end{aligned}
cos ( − θ ) = r x = cos θ .
サインの場合は点 A ( x , y ) A(x, y) A ( x , y ) A ′ ( x , − y ) A'(x, -y) A ′ ( x , − y ) y y y sin ( − θ ) = − sin θ \sin (- \theta) = - \sin \theta sin ( − θ ) = − sin θ x x x cos ( − θ ) = cos θ \cos (- \theta) = \cos \theta cos ( − θ ) = cos θ
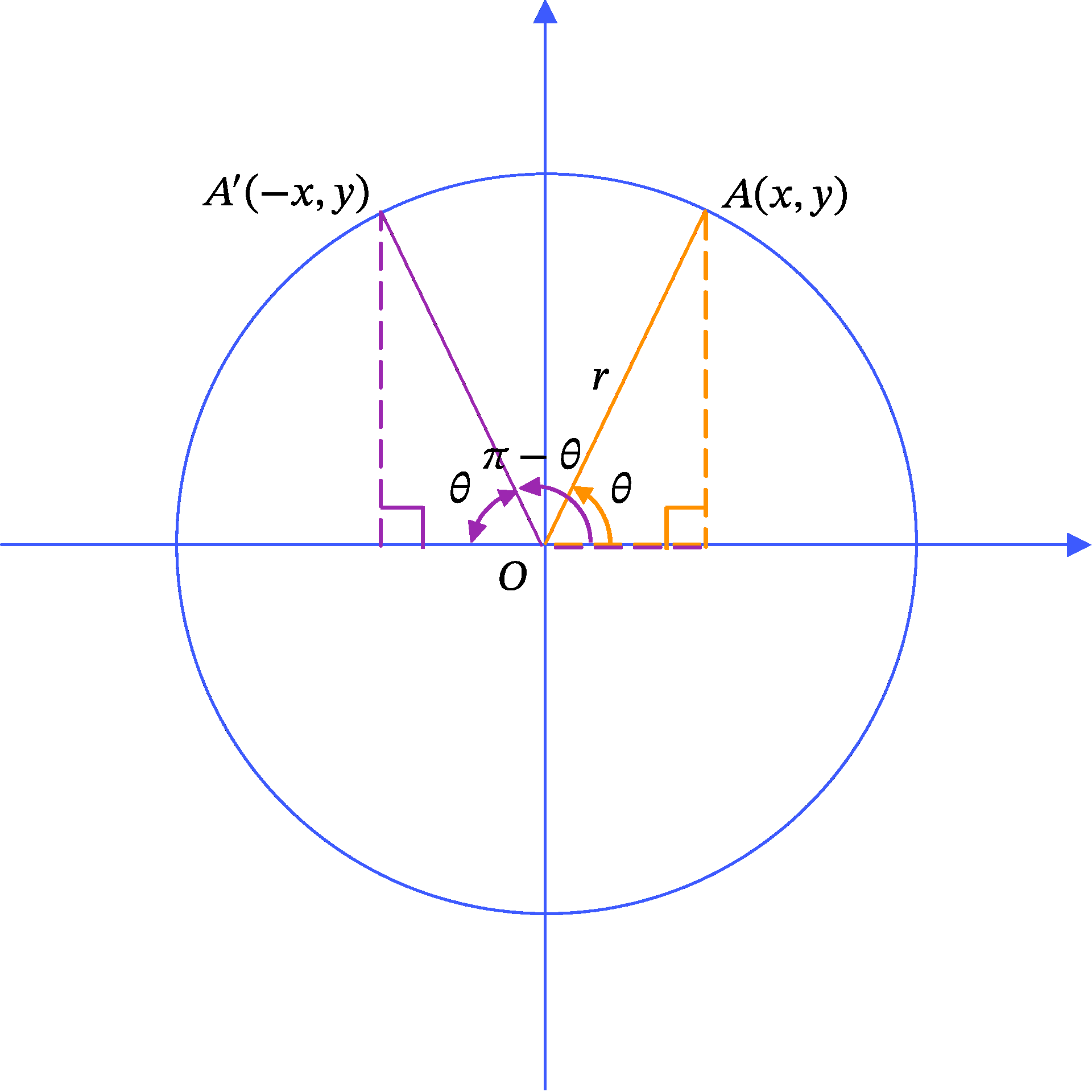
sin ( π − θ ) = sin θ \sin{(\pi - \theta)} = \sin{\theta} sin ( π − θ ) = sin θ
− θ - \theta − θ Figure 3 を見てください。
今回は点 A ′ A' A ′ ( − x , y ) (-x, y) ( − x , y ) π − θ \pi - \theta π − θ π \pi π θ \theta θ O O O θ \theta θ
では三角関数の定義に従ってサインを計算してみましょう。
sin ( π − θ ) = y r = sin θ .
\begin{aligned}
\sin(\pi - \theta) &= \frac{y}{r} \\
&= \sin \theta.
\end{aligned}
sin ( π − θ ) = r y = sin θ .
簡単に示せました。三角関数の定義に従っていけば問題なく導けますね。コツとしては、 π − θ \pi - \theta π − θ θ \theta θ
tan ( π 2 − θ ) = 1 tan θ \tan{\left(\frac{\pi}{2} - \theta \right)} = \frac{1}{\tan{\theta}} tan ( 2 π − θ ) = t a n θ 1
π 2 \frac{\pi}{2} 2 π Figure 4 のように、点 A ′ A' A ′
コツとしては一度 x x x π 2 \frac{\pi}{2} 2 π θ \theta θ π 2 − θ \frac{\pi}{2} - \theta 2 π − θ
この時できる点 A ′ A' A ′ A A A r r r O O O π 2 − θ \frac{\pi}{2} - \theta 2 π − θ π \pi π A ′ A' A ′
π − π 2 − ( π 2 − θ ) = θ
\pi - \frac{\pi}{2} - \left(\frac{\pi}{2} - \theta \right) = \theta
π − 2 π − ( 2 π − θ ) = θ
「直角三角形において斜辺と他の1つの鋭角がそれぞれ等しい」ので、紫とオレンジの三角形は合同といえます。したがって点 A ′ A' A ′ A ′ ( y , x ) A'(y, x) A ′ ( y , x )
この点 A ′ A' A ′
tan ( π 2 − θ ) = x y = 1 y x = 1 tan θ .
\begin{aligned}
\tan \left( \frac{\pi}{2} - \theta \right) &= \frac{x}{y} \\
&= \frac{1}{\frac{y}{x}} \\
&= \frac{1}{\tan \theta}.
\end{aligned}
tan ( 2 π − θ ) = y x = x y 1 = tan θ 1 .
これで導出できました。もちろん tan θ = 0 \tan \theta = 0 tan θ = 0
加法定理を使った導出
加法定理を使って導出する公式についても少し紹介しておきます。
Equation 13 : sin 2 θ = 2 sin θ cos θ \sin{2\theta} = 2\sin\theta\cos\theta sin 2 θ = 2 sin θ cos θ
Theorem 1 sin ( A + B ) = sin A cos B + cos A sin B \sin(A + B) = \sin A \cos B + \cos A \sin B sin ( A + B ) = sin A cos B + cos A sin B A = B = θ A = B = \theta A = B = θ A + B = θ + θ = 2 θ A + B = \theta + \theta = 2\theta A + B = θ + θ = 2 θ
sin ( A + B ) = sin A cos B + cos A sin B sin ( θ + θ ) = sin θ cos θ + cos θ sin θ ( ∵ A = B = θ ) sin ( 2 θ ) = 2 sin θ cos θ .
\begin{aligned}
\sin(A + B) &= \sin A \cos B + \cos A \sin B \\
\sin(\theta + \theta) &= \sin \theta \cos \theta + \cos \theta \sin \theta \qquad (\because A = B = \theta) \\
\sin(2 \theta) &= 2 \sin \theta \cos \theta.
\end{aligned}
sin ( A + B ) sin ( θ + θ ) sin ( 2 θ ) = sin A cos B + cos A sin B = sin θ cos θ + cos θ sin θ ( ∵ A = B = θ ) = 2 sin θ cos θ .
あっさりと導けました。
Equation 14 : cos 2 θ = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ \cos{2\theta} = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2\sin^2\theta cos 2 θ = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ
Equation 14 の基本的な形は cos 2 θ = cos 2 θ − sin 2 θ \cos{2\theta} = \cos^2\theta - \sin^2\theta cos 2 θ = cos 2 θ − sin 2 θ
先ほどのサインの場合(Equation 13 ) と同様に、 A = B = θ A = B = \theta A = B = θ
cos ( A + B ) = cos A cos B − sin A sin B cos ( θ + θ ) = cos θ cos θ − sin θ sin θ cos ( 2 θ ) = cos 2 θ − sin 2 θ .
\begin{aligned}
\cos(A + B) &= \cos A \cos B - \sin A \sin B \\
\cos(\theta + \theta) &= \cos \theta \cos \theta - \sin \theta \sin \theta \\
\cos (2 \theta) &= \cos^2 \theta - \sin^2 \theta.
\end{aligned}
cos ( A + B ) cos ( θ + θ ) cos ( 2 θ ) = cos A cos B − sin A sin B = cos θ cos θ − sin θ sin θ = cos 2 θ − sin 2 θ .
これが1つ目の公式です。他2つの公式はコサインのみ、サインのみでそれぞれ表されています。したがって「サインを消す」、「コサインを消す」という操作をそれぞれ行えばよさそうです。サインとコサインをつなぐ公式は Equation 1 ですので、これを使いましょう。
cos ( 2 θ ) = cos 2 θ − sin 2 θ = cos 2 θ − ( 1 − cos 2 θ ) = 2 cos 2 θ − 1.
\begin{aligned}
\cos (2 \theta) &= \cos^2 \theta - \sin^2 \theta \\
&= \cos^2 \theta - (1 - \cos^2 \theta) \\
&= 2 \cos^2 \theta - 1.
\end{aligned}
cos ( 2 θ ) = cos 2 θ − sin 2 θ = cos 2 θ − ( 1 − cos 2 θ ) = 2 cos 2 θ − 1.
サインの場合も同様に示せます。
cos ( 2 θ ) = cos 2 θ − sin 2 θ = ( 1 − sin 2 θ ) − sin 2 θ = 1 − 2 sin 2 θ .
\begin{aligned}
\cos (2 \theta) &= \cos^2 \theta - \sin^2 \theta \\
&= (1 - \sin^2 \theta) - \sin^2 \theta \\
&= 1 - 2 \sin^2 \theta.
\end{aligned}
cos ( 2 θ ) = cos 2 θ − sin 2 θ = ( 1 − sin 2 θ ) − sin 2 θ = 1 − 2 sin 2 θ .
まとめ: 公式を自然に覚えるための方法
以上のように、三角関数の公式は定義や加法定理を使って、簡単に導き出せることがわかりました。このような公式の導出に慣れておくと、語呂合わせによる単なる丸暗記と比べ、公式間のつながりや公式自体の理解、そしてこの分野で良く行う変形など多くのことが学べます。
本記事で確認したように、三角関数の公式は、「(1)三角関数の定義を使って証明されるグループ 」と「(2)加法定理を使って証明されるグループ 」に分類することができます。どの公式がどちらのグループに分類されるかを改めて確認しておきましょう。
公式の導出方法は一度行っただけで自然と身につくものではありません。繰り返し導出を行ってみてください。重要なことは公式の導出過程で、「なぜそのように考えたかを自分なりに整理しておくこと 」です。「次回自分で導出できるためには、何を知っておけばよいか 」このことを常に考えながら取り組んでみてください。公式の丸暗記と違い、考え方というのは理解してしまえば案外忘れづらいものです。
合わせて公式を使った問題を繰り返し解いてください。問題を解く際には公式を見ながらでも構いません。繰り返し公式を使うことで自然と公式が身についてきます。またその都度公式の導出 を行ってもよいでしょう。公式を忘れていてもすぐに導出できます。
この記事では一部の公式のみを扱いましたが、他の公式についても導出をすぐに行えるようにしておくと良いですね。
公式の導出は遠回りなようですが、本気で数学の力を高めたいのなら、避けては通れない道です。そして単なる丸暗記と比べ、三角関数における基本的な考え方や代表的な式の変形方法など、応用へつながるさまざまな重要なことを学べます。丸暗記ではなく、公式の導出と繰り返しの問題演習を通じて自然と公式を覚えていきましょう。