It is essential to understand the proofs of trigonometric identities rather than merely memorising them. This ensures that you can derive them quickly when needed, and you do not even need to memorise them. In this article, we will utilise the definitions of trigonometric functions to prove the following fundamental identities.
\sin^2{\theta} + \cos^2{\theta} = 1 \tag{1}
\tan \theta = \frac{\sin{\theta}}{\cos{\theta}} \tag{2}
1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}} \tag{3}
1 Proof for \sin^2{\theta} + \cos^2{\theta} = 1
Trigonometric functions are defined using a circle. (Figure 1, Definition 1, and Definition of Trigonometric Functions).
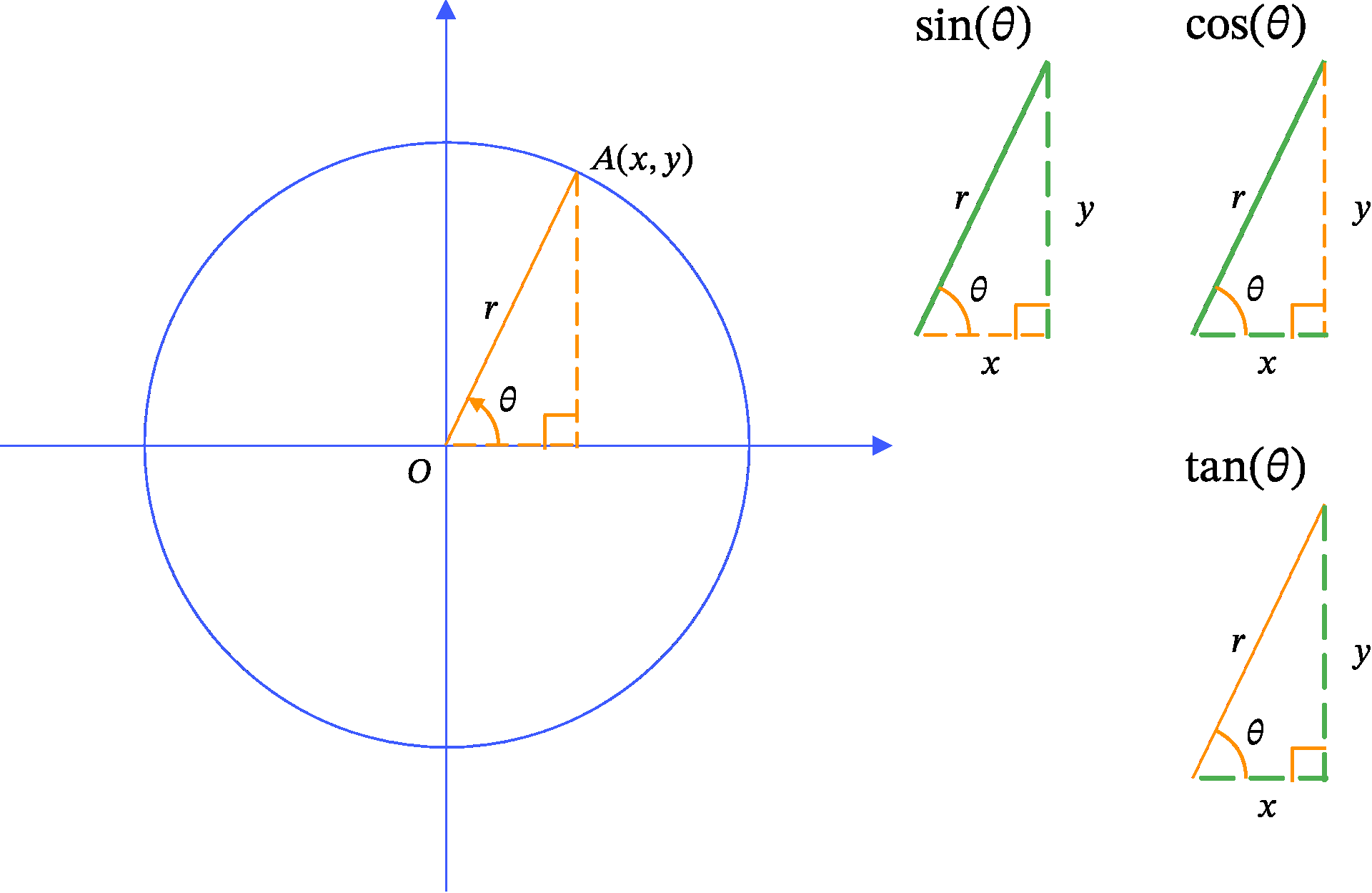
Definition 1 (Definition of Trigonometric Functions) \begin{aligned} \sin \theta &= \frac{y}{r}\\ \cos \theta &= \frac{x}{r}\\ \tan \theta &= \frac{y}{x} \end{aligned}
We can consider any point A on the circumference of the circle with coordinates x and y (Figure 1). Since a circle is a collection of points that are equidistant from a single point (the centre), we can apply the Pythagorean theorem to get the following equation:
x^2 + y^2 = r^2 \tag{4}
Note Equation 4 holds true for the coordinates of any points on the circumference of the circle.
Examining the definition of the trigonometric functions, we see that y is in \sin \theta and x is in \cos \theta. Therefore, if we compute the squares of these two functions and add them, we should arrive at x^2 + y^2, allowing us to apply Equation 4.
Now, let us add the squares of \sin \theta and \cos \theta.
\begin{aligned} \sin ^{2}\theta +\cos ^{2}\theta &= \left( \dfrac{y}{r}\right) ^{2}+\left( \dfrac{x}{r}\right) ^{2}\\ &=\dfrac{y^{2}}{r^{2}}+\dfrac{x^{2}}{r^{2}}\\ &=\dfrac{x^{2}+y^{2}}{r^{2}}\\ &=\dfrac{r^{2}}{r^{2}} \qquad \left( \because x^{2}+y^{2}=r^{2}\right) \\ &=1. \end{aligned}
Indeed, we have successfully derived Equation 1. We have proven this result straightforwardly from the definitions we have discussed. Essentially, Equation 1 expresses the relationship that the distance from the centre of the circle to any point on the circumference is equal to the radius.
2 Proof of \tan \theta = \frac{\sin{\theta}}{\cos{\theta}}
In proving an equation, it is often advantageous to begin with the more complex side of the equation. Thus, we will start our calculation on the right-hand side.
It is important to note that when \cos \theta = 0, the value of the right-hand side cannot be defined. Therefore, under the condition that \cos \theta \ne 0, according to Definition 1, the right-hand side can be expressed as follows:
\begin{aligned} \frac{\sin{\theta}}{\cos{\theta}} &= \frac{\frac{y}{r}}{\frac{x}{r}} \qquad (\text{if } \cos \theta \ne 0)\\ &= \frac{\frac{y}{r} \times r}{\frac{x}{r} \times r}\\ &= \frac{y}{x}. \end{aligned}
Here, since \tan \theta = \frac{y}{x}, we have proven \tan \theta = \frac{\sin{\theta}}{\cos{\theta}}.
3 Proof of 1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}}
By dividing the right-hand side of Equation 1 by \cos^2 \theta, we obtain \frac{1}{\cos^2 \theta} as a result. With this in mind, when \cos \theta \ne 0, we divide both sides of Equation 1 by \cos^2 \theta:
\begin{aligned} \sin ^2 \theta + \cos ^2 \theta &= 1\\ \frac{\sin ^2 \theta + \cos ^2 \theta}{\cos^2 \theta} &= \frac{1}{\cos^2 \theta} \qquad (\text{if } \cos \theta \ne 0)\\ \frac{\sin ^2 \theta}{\cos^2 \theta} + \frac{\cos^2 \theta}{\cos^2 \theta} &= \frac{1}{\cos^2 \theta}. \end{aligned} \tag{5}
Here, we transform Equation 5, using \tan \theta = \frac{y}{x} (Definition 1):
\begin{aligned} \left(\frac{\sin \theta}{\cos \theta}\right)^2 + \frac{\cos^2 \theta}{\cos^2 \theta} &= \frac{1}{\cos^2 \theta}\\ \left( \tan \theta \right)^2 + 1 &= \frac{1}{\cos^2 \theta}\\ 1 + \tan^2{\theta} &= \frac{1}{\cos^2{\theta}}. \end{aligned}
Now, we have proven Equation 3.
4 Conclusion
We have successfully proven the fundamental identities of trigonometric functions using their definitions. There are many other trigonometric identities, but it is essential to practise deriving them rather than merely memorising them. This practice enhances your understanding of trigonometric functions and aids in developing your problem-solving skills.
With just a few steps, these identities can be proven, so I encourage you to practise regularly.



