No More Memorising Trigonometric Identities: Just Derive Them

You possess numerous trigonometric identities, and many of you might struggle to recall them all. However, there is no reason for concern. In truth, you do not need to memorise each formula. By grasping the definitions of trigonometric functions and the addition formulae, you can easily derive a lot of the formulae.

In this article, we will begin by clarifying the meanings of trigonometric functions and the addition formulae. From these foundations, we will derive some trigonometric identities and structure the connections between these formulae. Finally, I will present a process that allows you to memorise the formulae naturally through comprehensive understanding, rather than depending only on memorisation without comprehension.

This article classifies the trigonometric formulae in the following manner for your reference:

• 1. A group proven using the definition of trigonometric functions
• 2. A group proven using the addition formulae

1 Definition of Trigonometric Functions

There are three trigonometric functions: sine (\sin()), cosine (\cos()), and tangent (\tan()). These originally represented the ratios of sides in a right-angled triangle. However, this limits their application to acute angles (from 0^\circ to 90^\circ). To handle more general angles, trigonometric functions are defined using a circle.

Please refer to Figure 1 to confirm the definitions of trigonometric functions.

In Figure 1, circles and points are created through the following steps.

1. Draw a circle with the centre at the origin O and a radius of r.
2. Add a point A to the circumference of this circle at random. The coordinates of point A are denoted as (x, y).
3. Draw a line segment OA with point A and the centre of the circle as its endpoints.
4. Let the angle between the x-axis and line segment OA be \theta. This angle \theta is measured counterclockwise from the positive direction of the x-axis.

Using these values of r, x, y, and \theta, we define the trigonometric functions:

• \sin(\theta) = \frac{y}{r}
• \cos(\theta) = \frac{x}{r}
• \tan(\theta) = \frac{y}{x}

Understanding these fundamental definitions will serve as a foundation for subsequent topics.

2 Addition Formulae

The addition formula is an important tool for connecting trigonometric functions with different angles. It is expressed:

With the angle A-B, the identities are also included in addition formulae, but it can be easily derived by substituting B with -B in Theorem 1; thus, I will omit it here.

The addition formulae and the definitions of trigonometric functions serve as a foundation for deriving other formulae. It is essential to remember the addition formula itself.

3 Classification of Trigonometric Identities

There are numerous identities associated with trigonometric functions, and it is essential to organise them. As previously noted, these identities can be readily obtained using the definitions of trigonometric functions and the addition formulae. In this article, following the classification of the trigonometric identities, I will emphasise several of them and demonstrate their derivation.

3.1 Formulae Derived from the Definition

These formulae can be derived from the definition of trigonometric functions.

\sin^2{\theta} + \cos^2{\theta} = 1 \tag{1}

\tan(\theta) = \frac{\sin{\theta}}{\cos{\theta}} \tag{2}

1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}} \tag{3}

\sin{(-\theta)} = -\sin{\theta} \tag{4}

\cos{(-\theta)} = \cos{\theta} \tag{5}

\tan{(-\theta)} = -\tan{\theta} \tag{6}

\sin{(\pi - \theta)} = \sin{\theta} \tag{7}

\cos{(\pi - \theta)} = -\cos{\theta} \tag{8}

\tan{(\pi - \theta)} = -\tan{\theta} \tag{9}

\sin{\left(\frac{\pi}{2} - \theta \right)} = \cos{\theta} \tag{10}

\cos{\left(\frac{\pi}{2} - \theta \right)} = \sin{\theta} \tag{11}

\tan{\left(\frac{\pi}{2} - \theta \right)} = \frac{1}{\tan{\theta}} \tag{12}

3.2 Formulae Derived from the Addition Formulae

These formulae can be obtained using the addition formulae.

Double Angle Formulae

\sin{2\theta} = 2\sin\theta\cos\theta \tag{13}

\cos{2\theta} = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2\sin^2\theta \tag{14}

\tan{2\theta} = \frac{2\tan\theta}{1 - \tan^2\theta} \quad (1 - \tan^2θ \neq 0) \tag{15}

Half Angle Formulae

\sin ^{2}\dfrac{\alpha }{2}=\frac{1 - \cos \alpha }{2} \tag{16}

\cos ^{2}\dfrac{\alpha }{2}=\dfrac{1+\cos \alpha }{2} \tag{17}

\tan ^{2}\dfrac{\alpha }{2}=\dfrac{1-\cos \alpha }{1+\cos \alpha } \tag{18}

Combining Trigonometric Functions

a\sin \theta + b\cos \theta =\sqrt{a^{2}+b^{2}} \sin \left( \theta +\alpha \right) \tag{19}

Here,

\begin{aligned} \cos \alpha &= \dfrac{a}{\sqrt{a^{2}+b^{2}}},\\ \sin \alpha &= \dfrac{b}{\sqrt{a^{2}+b^{2}}}. \end{aligned}

4 Derivation of Formulae

Alongside those mentioned previously, there are numerous equations associated with trigonometric functions. Memorising all of them can be quite challenging and, more crucially, does not promote true mathematical understanding. By grasping how a particular formula is constructed, one can identify the relationships between formulae and create a cohesive story. By structuring and understanding formulae within this context, we can achieve retention that is combined with understanding and practical skills, rather than just memorisation.

Thus, we will choose several formulae from those previously mentioned to demonstrate that they can indeed be derived from the definition or addition formulae. It is important to emphasise that detailed proofs are not the objective; instead, the focus is on enhancing our insight into the relationships among the formulae.

4.1 Derivation Using the Definition

4.1.1 Derivation of \sin^2{\theta} + \cos^2{\theta} = 1

Trigonometric functions are defined using a circle. A circle is a collection of points that are equidistant (at a distance r) from a single point (the centre). Therefore, for any point A on the circumference of the circle, the coordinates x and y satisfy the Pythagorean theorem, leading to the following equation.

x^2 + y^2 = r^2 \tag{20}

Now, when we look at the definitions of trigonometric functions, \sin \theta includes y, while cos theta includes x. This means that if we calculate the squares of these and add them together, we obtain x^2 + y^2, which suggests we can use Equation 20.

Therefore, let us try adding the squares of \sin \theta and \cos \theta.

\begin{aligned} \sin ^{2}\theta +\cos ^{2}\theta &= \left( \dfrac{y}{r}\right) ^{2}+\left( \dfrac{x}{r}\right) ^{2}\\ &=\dfrac{y^{2}}{r^{2}}+\dfrac{x^{2}}{r^{2}}\\ &=\dfrac{x^{2}+y^{2}}{r^{2}}\\ &=\dfrac{r^{2}}{r^{2}} \qquad \left( \because x^{2}+y^{2}=r^{2}\right) \\ &=1. \end{aligned}

Certainly, Equation 1 has been derived. I believe it can be easily obtained from the definition. Essentially, it can be described as a formula stating that the distance between the centre and any point on the circumference is the radius.

4.1.2 Derivation of 1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}}

Equation 1 represents the relationship between \sin \theta and \cos \theta. Now, what about the relationship between \cos \theta and \tan \theta? Dividing both sides of Equation 1 by \sin^2 \theta seems to leave \sin^2 theta behind, so to eliminate \sin \theta, let us try dividing both sides by \cos ^2 \theta (we are ignoring the case where \cos \theta = 0):

\begin{aligned} \sin ^2 \theta + \cos ^2 \theta &= 1 \\ \frac{\sin ^2 \theta}{\cos ^2 \theta} + \frac{\cos ^2 \theta}{\cos ^2 \theta} &= \frac{1}{\cos ^2 \theta} \\ \frac{\sin ^2 \theta}{\cos ^2 \theta} + 1 &= \frac{1}{\cos ^2 \theta}. \end{aligned} \tag{21}

\frac{\cos ^2 \theta}{\cos ^2 \theta} = 1, so it seems to resemble the equation above. The left side is still somewhat complicated. However, the squared form on the left side looks similar to Equation 2. From Equation 2,

\frac{\sin ^2 \theta}{\cos ^2 \theta} = \left( \frac{\sin \theta}{\cos \theta} \right)^2 = \tan^2 \theta

Therefore, it seems we can eliminate \sin \theta by using \tan \theta. Consequently, Equation 21 will appear as follows:

\begin{aligned} \frac{\sin ^2 \theta}{\cos ^2 \theta} + 1 &= \frac{1}{\cos ^2 \theta} \\ \tan ^2 \theta + 1 &= \frac{1}{\cos ^2 \theta} \end{aligned}

We have derived Equation 3.

4.1.3 Derivation of \sin{(-\theta)} = -\sin{\theta}, \cos{(-\theta)} = \cos{\theta}

In this type of formula, we consider the point A corresponding to \theta and the point A' corresponding to - \theta (Figure 2).

Using the definition of trigonometric functions, \sin (-\theta) is calculated based on the coordinates of point A'(x, -y), as follows.

\begin{aligned} \sin (-\theta) &= \frac{-y}{r} \\ &= - \frac{y}{r} \\ &= - \sin \theta. \end{aligned}

Using the definition of trigonometric functions with circles, we can derive this easily.

Let us also derive \cos{(- \theta)} = \cos{\theta}.

We will consider it similarly as before, but since we are calculating the cosine, this time we will use the x coordinate.

\begin{aligned} \cos (-\theta) &= \frac{x}{r} \\ &= \cos \theta. \end{aligned}

With sine, the sign of the y coordinate changes between point A(x, y) and point A'(x, -y), leading to sin (- \theta) = - \sin \theta. For cosine, there is no change in the x coordinate, so \cos (- \theta) = \cos \theta, yielding the same value. By applying the definitions of trigonometric functions, you can easily recall the identities, or you are not even required to memorise them.

4.1.4 Derivation of \sin{(\pi - \theta)} = \sin{\theta}

You can derive this in a manner similar to when considering -theta. Please refer to Figure 3 for further clarification.

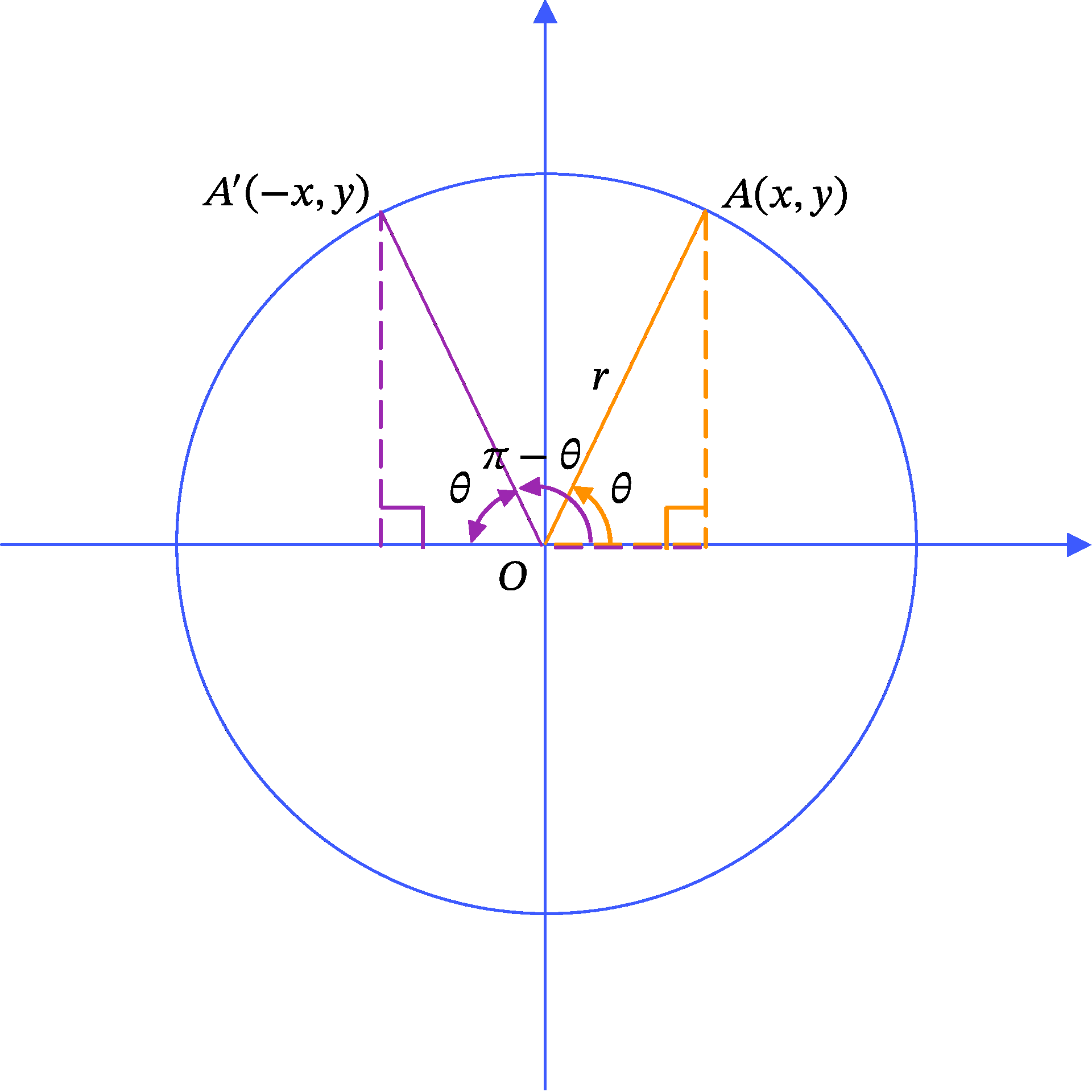
Please note that the coordinates of point A' are (-x, y). The purple right triangle and the orange right triangle are congruent. Consider \pi - \theta as an angle that initially measures \pi, from which we rotate clockwise by an angle of \theta. Consequently, the angle around point O in the purple triangle is \theta. Since the hypotenuse of the right triangle corresponds to the radius of the circle, these lengths are equal. Thus, we can reveal that the purple triangle and the orange triangle are congruent, given that in a right triangle, if a hypotenuse and an acute angle are equal to those in another triangle, then the triangles are congruent.

Now, let us calculate the sine according to the definitions of trigonometric functions.

\begin{aligned} \sin(\pi - \theta) &= \frac{y}{r} \\ &= \sin \theta. \end{aligned}

We have proved this easily. By following the definitions of trigonometric functions, you can derive the results with no difficulty. A useful tip is to eliminate \pi - \theta from the equation and focus on using \theta.

4.1.5 Derivation of \tan{\left(\frac{\pi}{2} - \theta \right)} = \frac{1}{\tan{\theta}}

In cases involving \frac{\pi}{2}, you need some familiarity with the thinking process. To summarise, as illustrated in Figure 4, you can derive this formula by considering the tangent in relation to the coordinates of point A'.

As a guiding principle, consider taking an angle of \frac{\pi}{2} in the counterclockwise direction from the positive direction of the x-axis, and then returning by an angle of \theta. The size of the angle will be \frac{\pi}{2} - \theta.

The resulting point A' forms a purple triangle that is congruent to the orange triangle containing point A. Both triangles are right triangles, with the length of the hypotenuse being equal to the radius r of the circle. In the purple triangle, the angle surrounding point O measures \frac{\pi}{2} - \theta, as previously discussed. Since the sum of the interior angles of a triangle is \pi radians, the sizes of the remaining angles around point A' can be determined accordingly:

\pi - \frac{\pi}{2} - \left(\frac{\pi}{2} - \theta \right) = \theta

In a right-angled triangle, the hypotenuse and one of the acute angles are equal, which shows that the purple and orange triangles are congruent. Therefore, the coordinates of point A' are given by A'(y, x). Is that clear?

Considering the tangent using the coordinates of this point A', we can express it:

\begin{aligned} \tan \left( \frac{\pi}{2} - \theta \right) &= \frac{x}{y} \\ &= \frac{1}{\frac{y}{x}} \\ &= \frac{1}{\tan \theta}. \end{aligned}

We have successfully derived this result. However, please note that this formula does not hold when \tan \theta = 0.

4.2 Derivation Using the Addition Formulae

I would also like to briefly introduce the formulae derived using the addition formulae.

4.2.1 Derivation of Equation 13: \sin{2\theta} = 2\sin\theta\cos\theta

Let us consider the addition formula for sine, which is expressed as \sin(A + B) = \sin A \cos B + \cos A \sin B. When we set A = B = \theta, we find that A + B becomes \theta + \theta = 2 \theta. This allows us to create an angle of the same magnitude as the one in the formula. Let us apply the addition formula:

\begin{aligned} \sin(A + B) &= \sin A \cos B + \cos A \sin B \\ \sin(\theta + \theta) &= \sin \theta \cos \theta + \cos \theta \sin \theta \qquad (\because A = B = \theta) \\ \sin(2 \theta) &= 2 \sin \theta \cos \theta. \end{aligned}

We have proved them with ease.

4.2.2 Derivation of Equation 14: \cos{2\theta} = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2\sin^2\theta

The most basic form of Equation 14 is given by \cos{2 \theta} = \cos^2 \theta - \sin^2 \theta. The other two formulae can be derived directly from this equation.

Similar to the case of sine discussed earlier (refer to Equation 13), let us consider the scenario where A = B = \theta.

\begin{aligned} \cos(A + B) &= \cos A \cos B - \sin A \sin B \\ \cos(\theta + \theta) &= \cos \theta \cos \theta - \sin \theta \sin \theta \\ \cos (2 \theta) &= \cos^2 \theta - \sin^2 \theta. \end{aligned}

This is the first formula. The other two formulae are expressed solely in terms of cosine and sine, respectively. Therefore, it seems appropriate to perform the operations of eliminating sine and eliminating cosine. The formula that connects sine and cosine is Equation 1, so let us utilise this.

\begin{aligned} \cos (2 \theta) &= \cos^2 \theta - \sin^2 \theta \\ &= \cos^2 \theta - (1 - \cos^2 \theta) \\ &= 2 \cos^2 \theta - 1. \end{aligned}

The same can be shown with sine.

\begin{aligned} \cos (2 \theta) &= \cos^2 \theta - \sin^2 \theta \\ &= (1 - \sin^2 \theta) - \sin^2 \theta \\ &= 1 - 2 \sin^2 \theta. \end{aligned}

5 Summary

As we have seen, the trigonometric identities can be readily derived through the definitions and the addition formulae. Familiarity with these derivations enables one to grasp much more than simple memorisation; it promotes an understanding of the relationships between formulae, the formulae themselves, and typical transformations in this area.

In this article, we classified trigonometric identities into two groups: (1) a group proven using the definitions of trigonometric functions and (2) a group proven using the addition formulae. It is beneficial to review which formulae belong to each category.

The journey towards mastering these formulae is not one that can be accomplished with a single attempt. I encourage you to immerse yourself in the derivation process repeatedly. It is essential to organise your understanding of the rationale behind the approach you used for the derivation. Reflect on the specific information you need to comprehend in order to derive the formula successfully in the future. By maintaining this mindset throughout your studies, you will find that cognitive processes—unlike simple memorisation—are relatively easy to retain once understood.

Engaging in consistent practice using the relevant mathematical formulae is essential for developing a solid understanding of the subject. It is entirely acceptable to refer back to these equations while addressing problems. By frequently applying the formulae, you will naturally become more familiar with them. Additionally, consider deriving the equations ocasionally when you use them; this process reinforces your comprehension and retention. Should you forget an equation, do not hesitate to derive it once more.

This article has focused on specific equations; however, it is equally beneficial to ensure that you are capable of deriving other equations as well.

Although the process of deriving identities may seem indirect, it is a vital path for those committed to enhancing their mathematical skills. This method, in contrast to mere memorisation, allows for a deeper understanding of foundational concepts in trigonometry. It also equips you with essential techniques for manipulating equations, thereby facilitating practical applications. Let us strive to remember the identities through both the derivation process and regular problem-solving practice, rather than relying solely on rote memorisation.

As you reflect on this approach, consider: how might deriving an equation deepen your understanding compared to simply recalling it? I encourage you to attempt deriving a formula you have previously memorised and observe the difference in your grasp of the underlying principles.