三角関数の公式は覚えるよりも、証明の方法を理解し、すぐに導出できるようにしておくことが肝心です。この記事では、三角関数の定義を使い、以下の三角関数の基本的な公式を証明します。
\sin^2{\theta} + \cos^2{\theta} = 1 \tag{1}
\tan \theta = \frac{\sin{\theta}}{\cos{\theta}} \tag{2}
1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}} \tag{3}
1 \sin^2{\theta} + \cos^2{\theta} = 1 の証明
三角関数は円を使って定義されます (Figure 1、 Definition 1 および、三角関数の定義)。
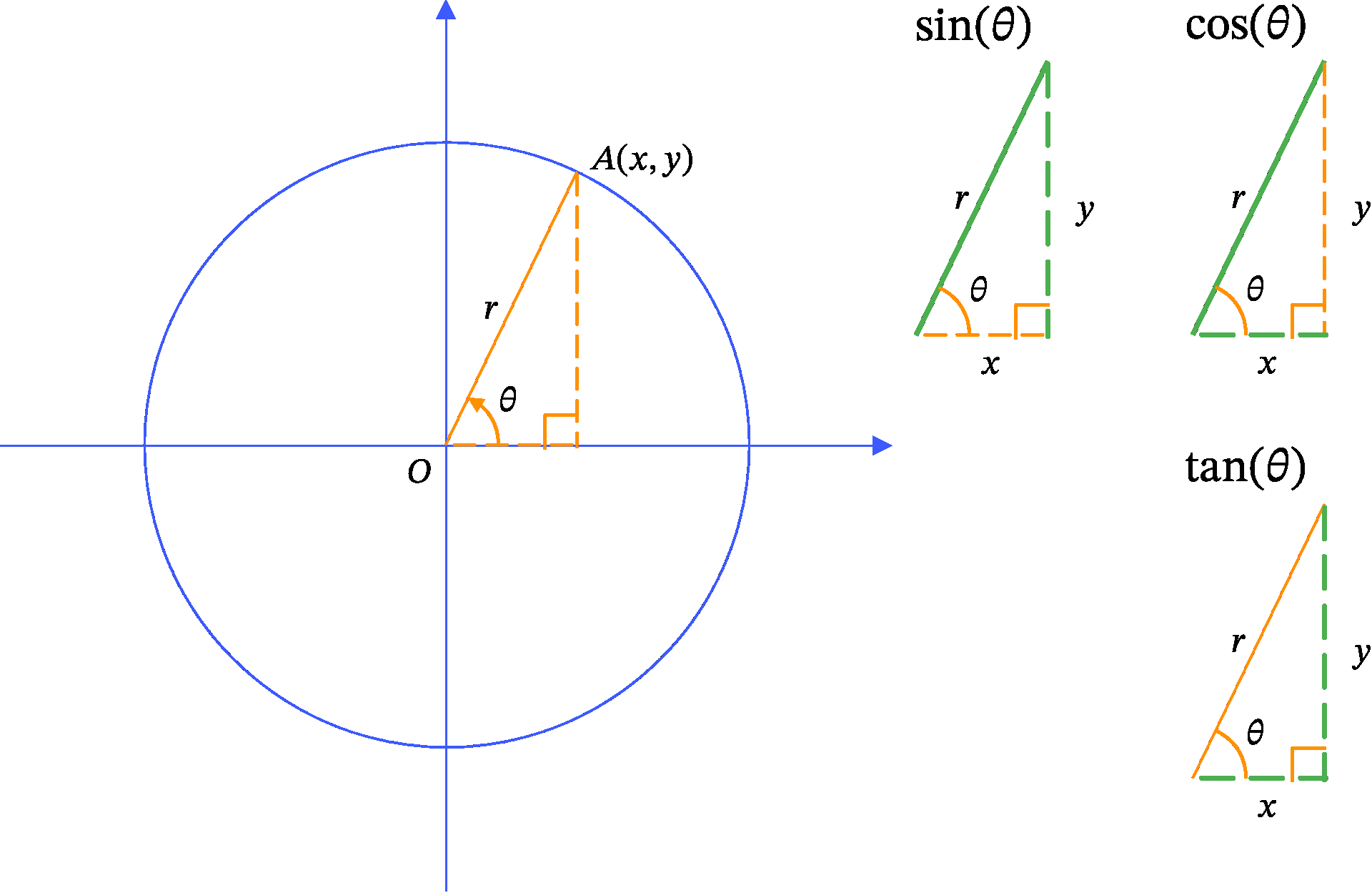
Definition 1 (三角関数の定義) \begin{aligned} \sin \theta &= \frac{y}{r}\\ \cos \theta &= \frac{x}{r}\\ \tan \theta &= \frac{y}{x} \end{aligned}
円は1点(中心)からの距離(r)が等しい点の集まりですから、 Figure 1 中にある円周上の任意の点である、点 A の座標 x と y について、三平方の定理より以下の式が成立します:
x^2 + y^2 = r^2 \tag{4}
ところで三角関数の定義を見ると、\sin \theta には y が、 \cos \theta には x が含まれています。つまりこれらの2乗を計算して足すと x^2 + y^2 が現れ、 Equation 4 を使えそうです。
したがって、 \sin \theta と \cos \theta の2乗同士を足してみましょう。
\begin{aligned} \sin ^{2}\theta +\cos ^{2}\theta &= \left( \dfrac{y}{r}\right) ^{2}+\left( \dfrac{x}{r}\right) ^{2}\\ &=\dfrac{y^{2}}{r^{2}}+\dfrac{x^{2}}{r^{2}}\\ &=\dfrac{x^{2}+y^{2}}{r^{2}}\\ &=\dfrac{r^{2}}{r^{2}} \qquad \left( \because x^{2}+y^{2}=r^{2}\right) \\ &=1. \end{aligned}
確かに Equation 1 が導かれました。定義からあっさり導けたと思います。実質的に、 Equation 1 は、中心と円周上の点の距離は半径であることを述べている式である、といえます。
2 \tan \theta = \frac{\sin{\theta}}{\cos{\theta}} の証明
等式の証明では左辺と右辺のうち、複雑な方から変形を行うと、式変形を進めやすいです。したがって、右辺から変形を始めます。
\cos \theta = 0 のときは右辺の式の値を定義できないことに注意すると、 \cos \theta \ne 0 のとき、Definition 1 より、右辺は以下のようになります:
\begin{aligned} \frac{\sin{\theta}}{\cos{\theta}} &= \frac{\frac{y}{r}}{\frac{x}{r}} \qquad (\text{if } \cos \theta \ne 0)\\ &= \frac{\frac{y}{r} \times r}{\frac{x}{r} \times r}\\ &= \frac{y}{x}. \end{aligned}
ここで、 \tan \theta = \frac{y}{x} ですので、\tan \theta = \frac{\sin{\theta}}{\cos{\theta}} が証明できました。
3 1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}} の証明
Equation 1 の右辺を \cos^2 \theta で割ると、 \frac{1}{\cos^2 \theta} が現れます。これをヒントに、\cos \theta \ne 0 のとき、Equation 1 の両辺を \cos^2 \theta で割ります:
\begin{aligned} \sin ^2 \theta + \cos ^2 \theta &= 1\\ \frac{\sin ^2 \theta + \cos ^2 \theta}{\cos^2 \theta} &= \frac{1}{\cos^2 \theta} \qquad (\text{if } \cos \theta \ne 0)\\ \frac{\sin ^2 \theta}{\cos^2 \theta} + \frac{\cos^2 \theta}{\cos^2 \theta} &= \frac{1}{\cos^2 \theta}. \end{aligned} \tag{5}
ここで、 \tan \theta = \frac{y}{x} (Definition 1) を使い、 Equation 5 を変形します:
\begin{aligned} \left(\frac{\sin \theta}{\cos \theta}\right)^2 + \frac{\cos^2 \theta}{\cos^2 \theta} &= \frac{1}{\cos^2 \theta}\\ \left( \tan \theta \right)^2 + 1 &= \frac{1}{\cos^2 \theta}\\ 1 + \tan^2{\theta} &= \frac{1}{\cos^2{\theta}}. \end{aligned}
これで、Equation 3 が証明できました。
4 まとめ
三角関数の基本的な公式を、三角関数の定義を使って証明しました。本記事で証明した以外にも、三角関数の公式 は多くありますが、基本的に丸暗記するのではなく、すぐに導出できるように練習しておくことが、三角関数の理解に、そして応用力の形成に重要です。少しのステップで証明できますので、よく練習しておきましょう。









