二次関数のグラフは放物線という図形で表されます。放物線は、自然界や工学、経済学などさまざまな分野で見られる形状であり、特にその頂点は放物線の特徴を理解するうえで、非常に重要です。放物線の頂点は単なるグラフ上の一点ではなく、実世界の様々な現象を理解するうえで非常に重要な要素です。例えば物体を投げ上げたときの最高点の位置や、経済的収益を最大化する点は、この頂点で表されます。
しかし、放物線の頂点を求めることが難しいと感じることも少なくありません。この問題を解決するためには、放物線の頂点を求めるための明確なステップを整理することが不可欠です。本記事では、最初に二次関数のグラフである放物線の性質や、実世界に見られる放物線で表される現象を紹介し、放物線の頂点を求めることの重要性を理解します。そして放物線の頂点を求めるための計算手順を、例を交えて分かりやすく解説します。
1 放物線とは何か?
二次関数との関係において、放物線は二次関数のグラフとして描かれる形状です。二次関数は一般的には以下の式で表されます。
y = ax^2 + bx + c
一般的に x は任意の実数と考えて差し支えありません。この式において、a は放物線の開き具合を決定し、b と c は放物線の位置を調整します。放物線の形状は x^2 の項の係数 a の符号によって大きく変化します。a>0 の時は”下に凸”、 a < 0 の時は”上に凸”とそれぞれ呼ばれます。“凸”はでっぱりのことです。確かに a > 0 の時はでっぱりが下に、 a < 0 の時はでっぱりが上に見られますね (Figure 1)。 放物線の頂点は、 (a) においては放物線の最も低い部分に、 (b) では最も高い部分に見られます。また放物線の特徴として対称性が挙げられます。つまり、頂点を中心に左右対称の形状を持ちます。
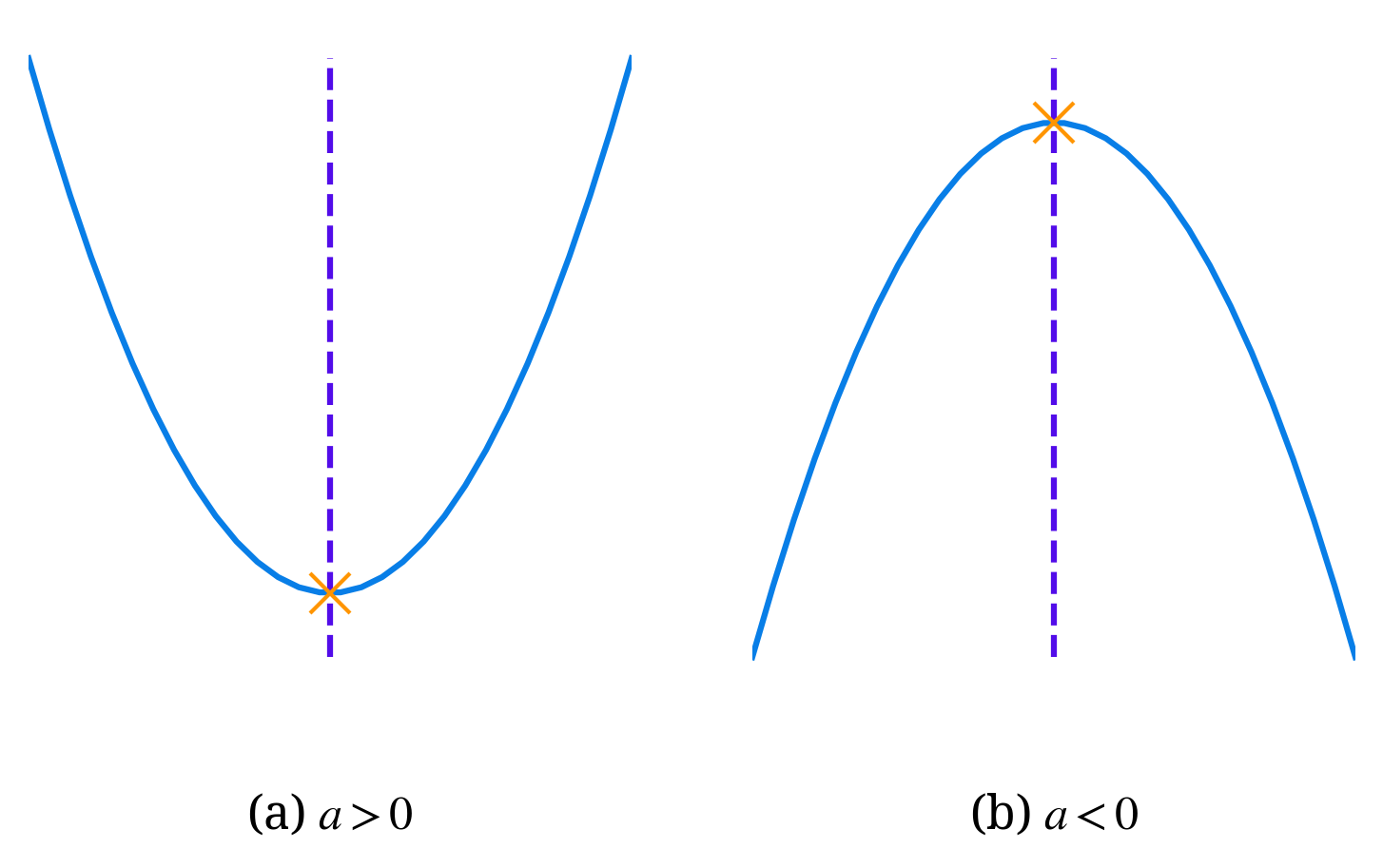
(a) a > 0: 下に凸. (b) a < 0: 上に凸. 紫のライン: 放物線の対称の軸, オレンジのクロスマーク: 放物線の頂点.
2 放物線の頂点が重要となる実例: 投げ上げられた物体の位置
投げ上げられた物体の位置は、放物線を使って表すことができます。投げ上げられた物体はどこまでも上昇するわけではなく、地球の重力によって減速し、やがて地面に向かって落ちていきます。この時物体が到達する最高点は、物体の移動した跡が描く放物線の頂点になります。
Figure 2 は投げ上げた物体の移動を表したシミュレーション結果です。青色の点で表された物体が上昇し、やがて落下していく様子が確認できます。オレンジ色の三角形はこの物体が移動した跡を表します。たしかに放物線を描いていますね。グラフを見ると、おおよそ10m横に移動したところで、高さが最大になりそうだとわかります。
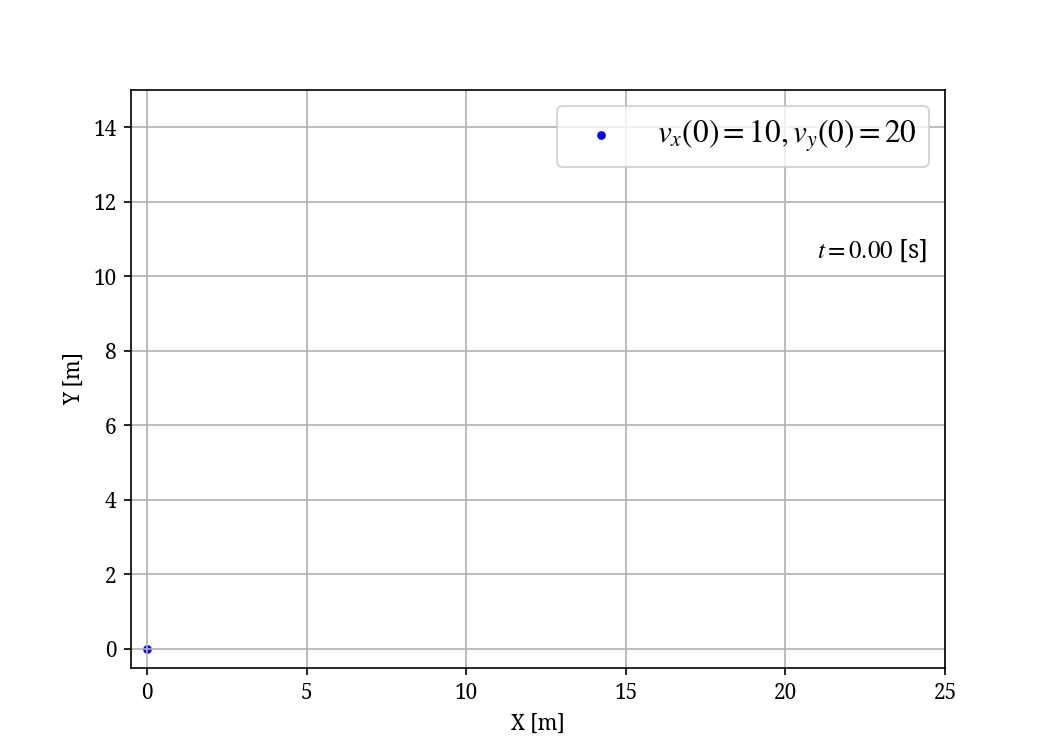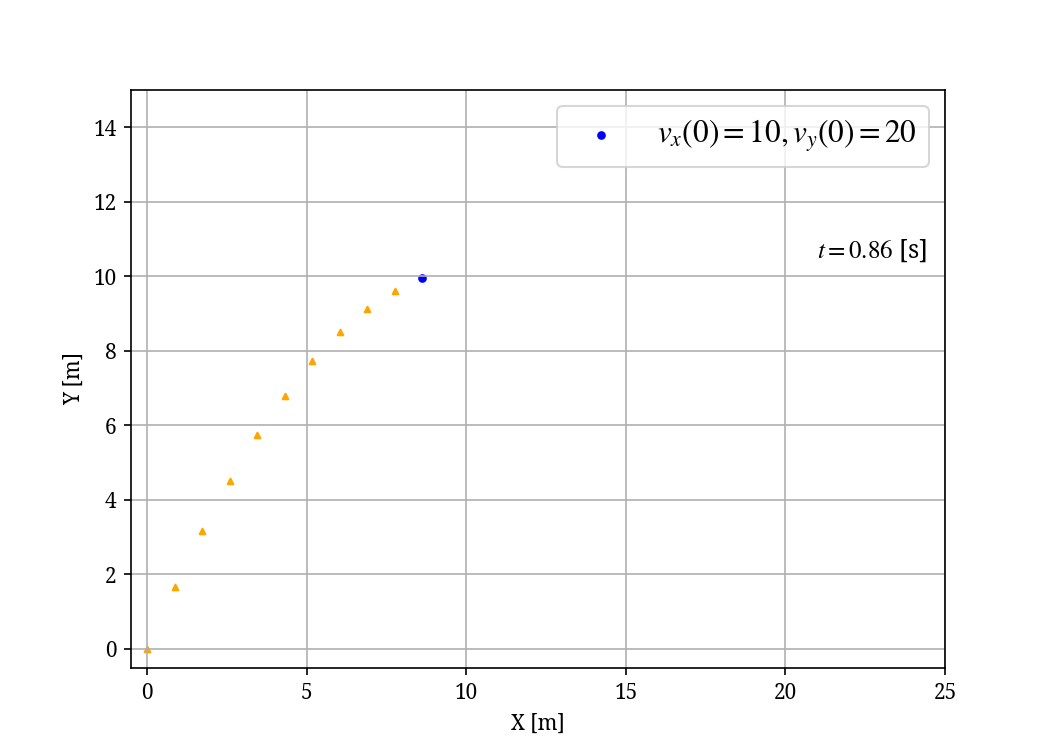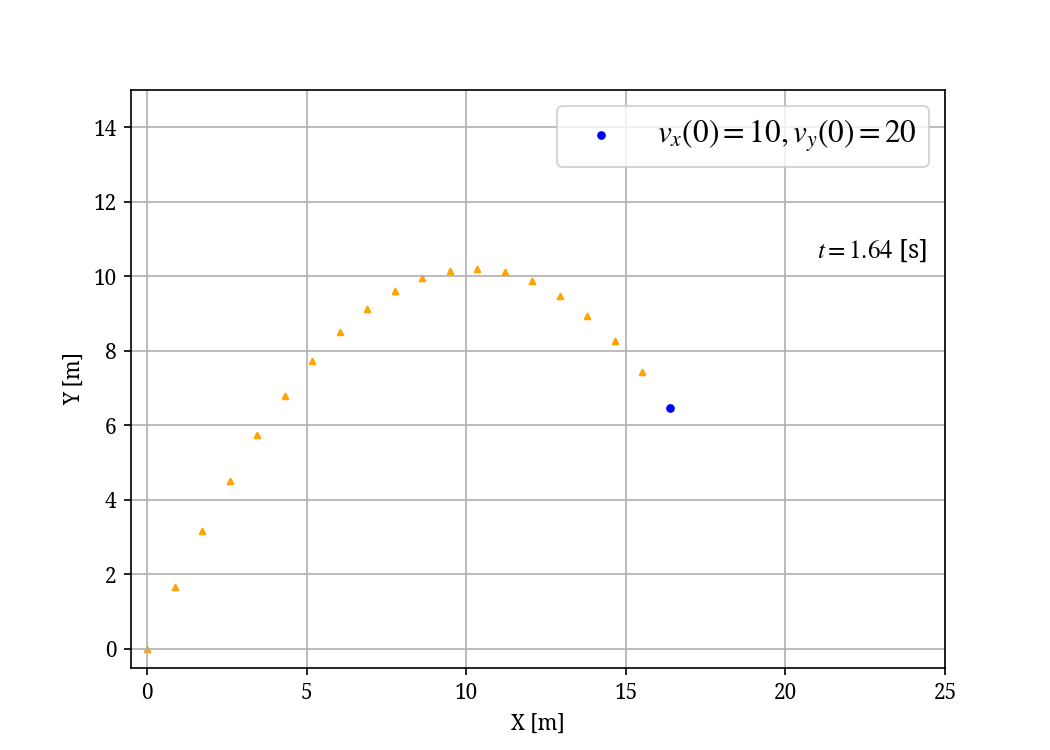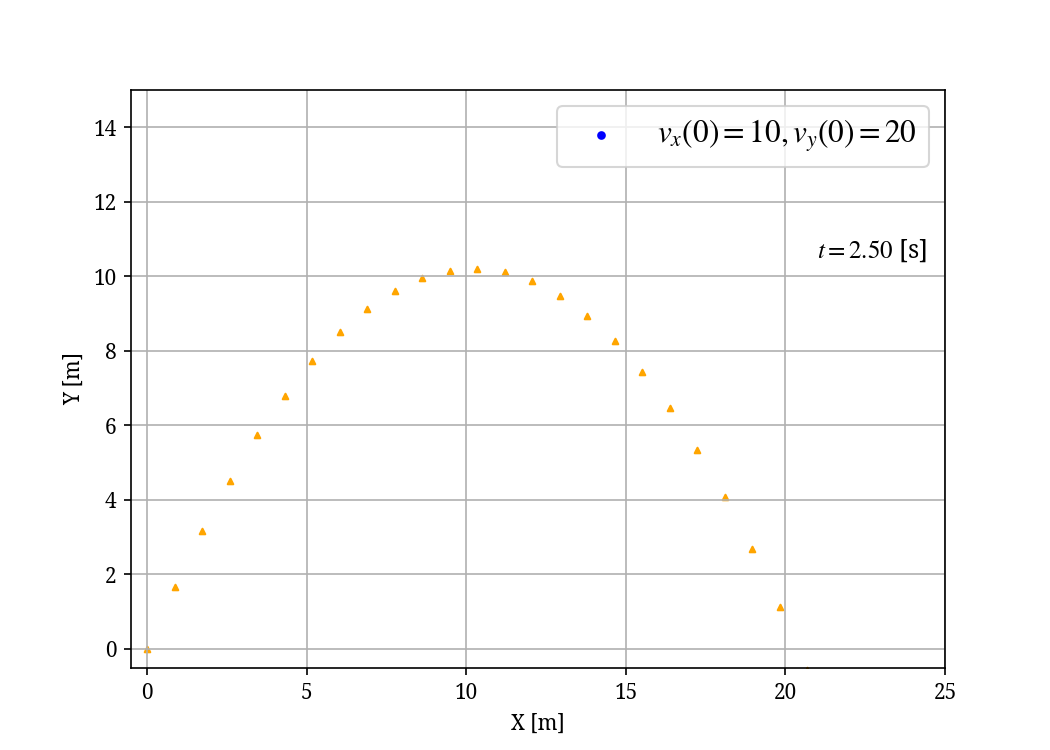
投げ上げられた物体の位置は放物線で表される。青色の丸: 投げ上げられた物体。オレンジ色の三角形: 物体の軌跡。
このように放物線は実世界における現象とも結びついた概念であり、その頂点はそのような現象の特徴を理解するうえで、重要な要素といえます。
3 頂点を見つけるためのステップ
では放物線の頂点を見つけるための過程を、ステップに分けて確認してみましょう。本記事ではCase 1と Case 2の2つの場合において放物線の頂点の座標を求める方法をご紹介します。
3.1 Case 1: y = a(x - b)^2 + c の形で二次関数が与えられた場合
この形は二次関数のグラフとしての放物線の頂点を求めるうえで、最も重要な形式です。結論としましては、この時放物線の頂点の座標は (b, c) となります。以下のようなステップで頂点の座標を見つけましょう。
- (x - b)^2 の部分を見る。
- x の後ろの部分、- b の符号を反転させる。-b \rightarrow b。これが頂点の x 座標となる。
- x を含んでいない部分(定数項)を見る。ここでは c の部分。
- この c が頂点の y 座標となる。
いくつか例を見て上記のステップを理解しましょう。
Example 1
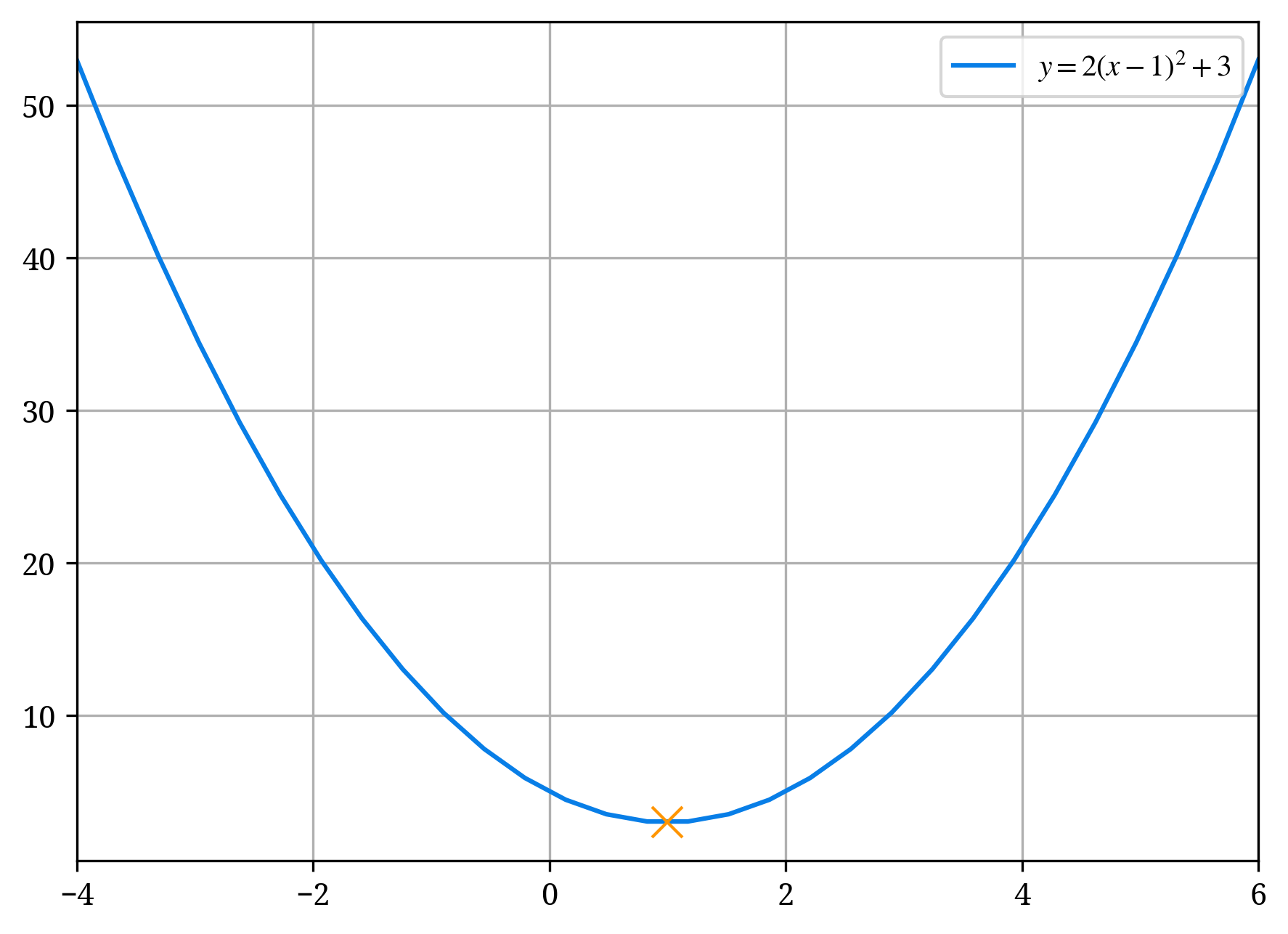
y = 2(x - 1)^2 + 3
- (x - 1)^2 を見る。
- x の後ろの部分、 -1 の符号を反転させ、1 を得る。これが頂点の x 座標である。
- x を含んでいない部分(定数項)を見る。ここでは 3 の部分。
- 3 が頂点の y 座標となる。
したがって、頂点の座標は (1, 3) となります。
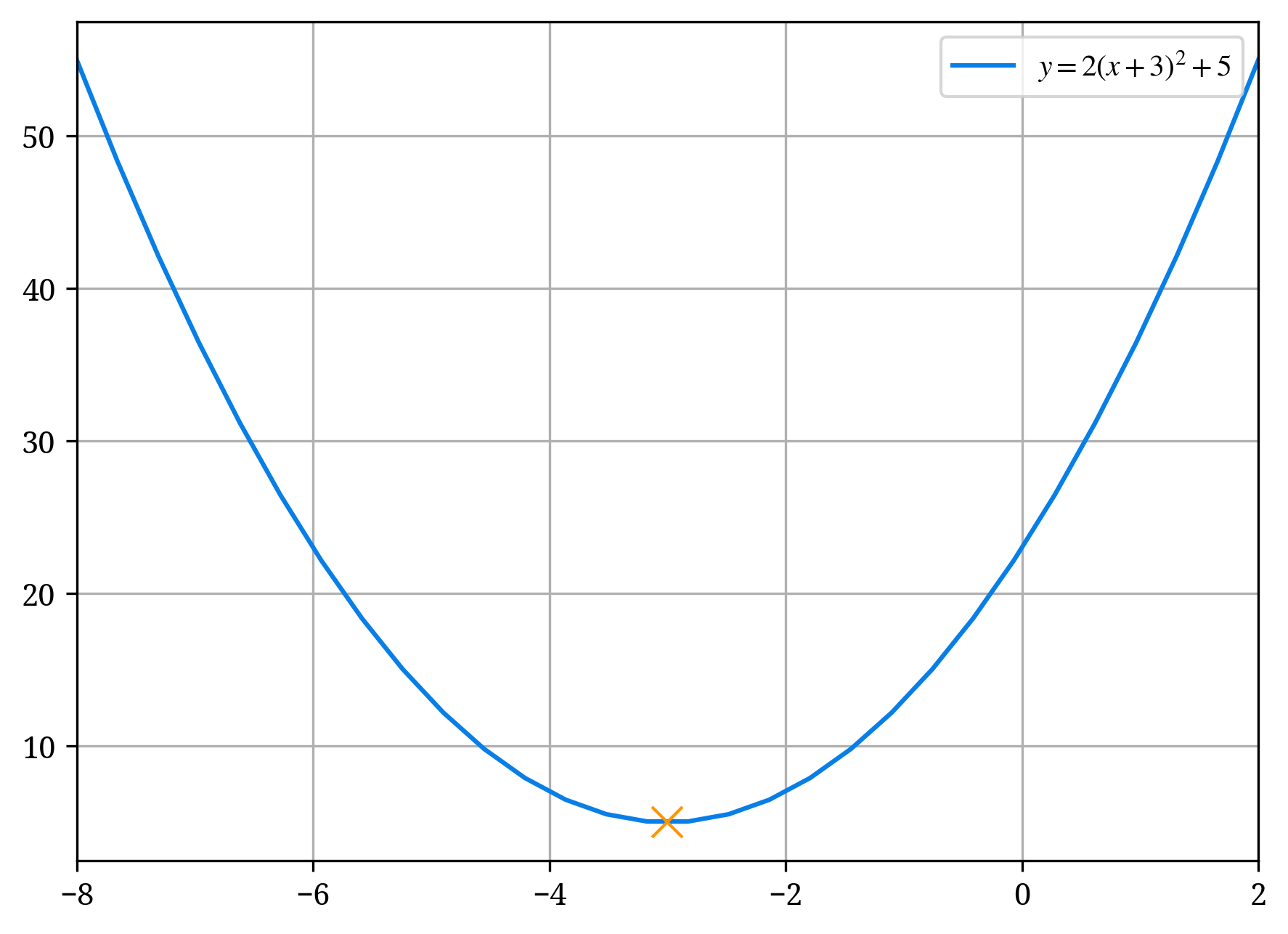
y = 2(x + 3)^2 + 5
- (x + 3)^2 を見る。
- x の後ろの部分、+3 の符号を反転させ、-3 を得る。これが頂点の x 座標である。
- x を含んでいない部分(定数項)を見る。ここでは 5 の部分。
- 5 が頂点の y 座標となる。
したがって、頂点の座標は (-3, 5) となります。
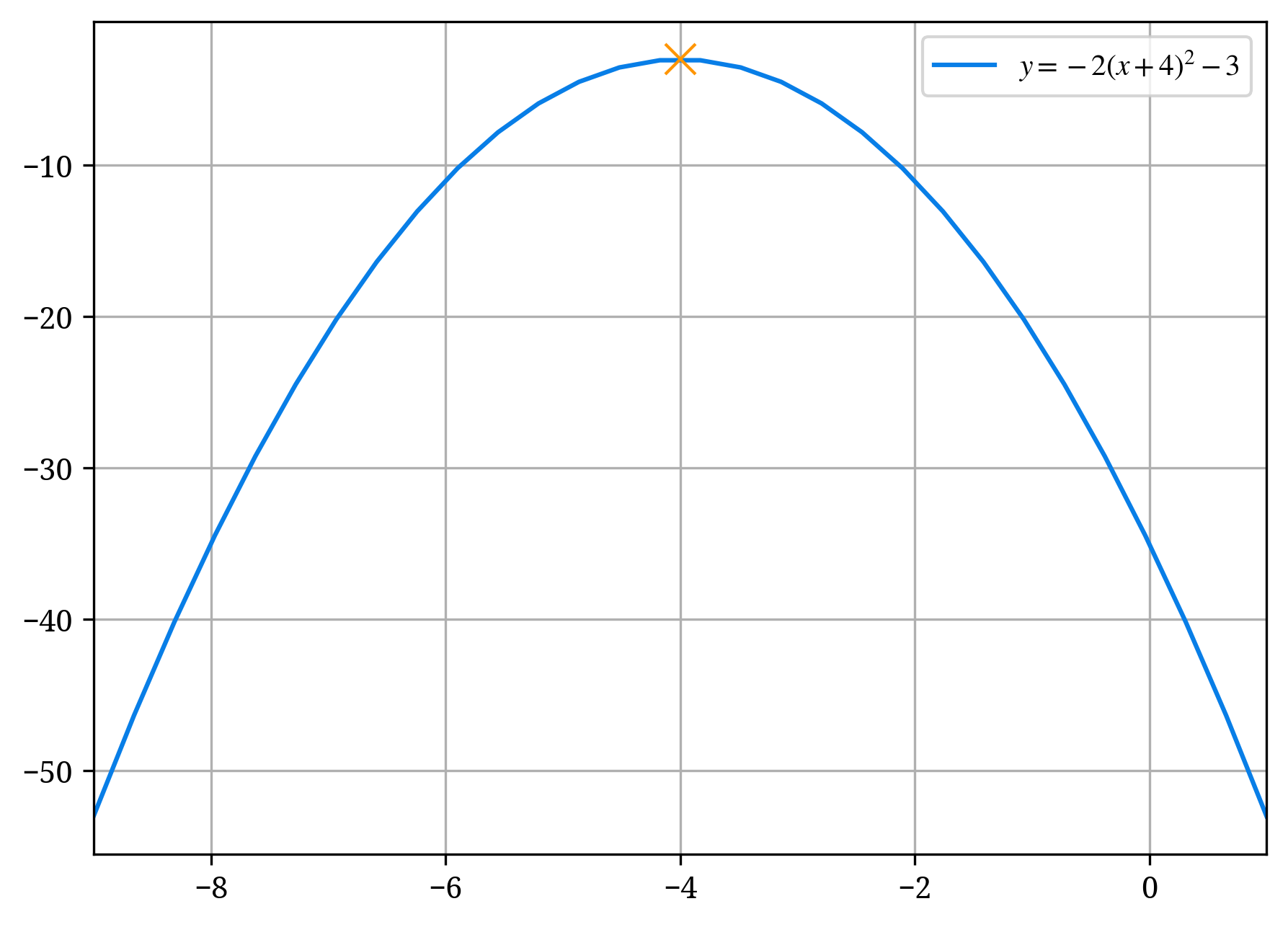
y = -2(x + 4)^2 - 3
- (x + 4)^2 を見る。
- x の後ろの部分、+4 の符号を反転させ、-4 を得る。これが頂点の x 座標である。
- x を含んでいない部分(定数項)を見る。ここでは -3 の部分。
- -3 が頂点の y 座標となる。
したがって、頂点の座標は (-4, -3) となります。
x 座標の方は符号を反転させる一方、 y 座標の場合はそのまま取り出してくる点に注意してください:
Tip 1: y = a(x - b)^2 + c の形で二次関数が与えられた場合の頂点の見つけ方
y = a(x - b)^2 + c において、
- x の後ろの部分の符号を反転させる: x 座標は b
- x を含んでいない部分(定数項)を取り出す: y 座標は c
以上のように y = a(x - b)^2 + c の形式から放物線の頂点を見つけることができます。ちなみに英語圏ではこの形式は “vertex form” (ヴァーテクス フォーム) と呼ばれることもあります。“vertex” は頂点という意味ですので、まさに頂点を見つけるための形式(“form”)というわけですね。
3.2 Case 2: y = ax^2 + bx + c の形で二次関数が与えられた場合
この形式は二次関数の一般形(general form)と呼ばれます。この形式ではCase 1 (Section 3.1 参照) の場合と異なり、頂点の座標は明らかではありません。しかし、Case 1 の形式に書き換えることで、頂点の座標を見つけることができます。ではどのようにして、一般形をCase 1 の vertex form へ書き換えればよいのでしょうか?
y = ax^2 + bx + c のままでは難しいので、具体例を通して書き換えを説明します。具体例として y = 2x^2 - 4x + 5 を扱います。
y = 2x^2 - 4x + 5 の vertex form への書き換え
- 2x^2 - 4x の部分に注目する。
- 2(x^2 - 2x) のように x^2 の項の係数でくくる。
- 2(x^2 - 2x) = 2(x - 1)^2 - 2 のように変形する。
- y = 2(x - 1)^2 - 2 + 5 = 2(x - 1)^2 + 3 となり、頂点の座標は (1, 3) となる。
この変形で一番複雑なステップは、 (3) における書き換えです。この変形では展開や因数分解で学習した以下の公式が重要です。
x^2 - 2ax + a^2 = (x - a)^2.
この公式中の a^2 を右辺に移項すると、
x^2 - 2ax = (x - a)^2 - a^2
となります。つまり x^2 - 2ax の形を (x - a)^2 のように変形します。すると右辺の (x - a)^2 の展開において a^2 が余計に生じるので、右辺ではそれを引いて等号を成立させています。
上式において a = 1 のとき、
x^2 - 2x = (x - 1)^2 - 1
となります。これを使うと、 (3) において以下の式が成立します。
\begin{aligned} 2(x^2 - 2x) &= 2((x - 1)^2 - 1) \qquad (\because x^2 - 2x = (x - 1)^2 - 1)\\ &= 2(x - 1)^2 - 2. \end{aligned}
これを使うと式全体の変形は以下のようになります。
\begin{aligned} 2x^2 - 4x + 5 &= 2(x^2 - 2x) + 5 \\ &= 2((x - 1)^2 - 1) + 5 \\ &= 2(x - 1)^2 - 2 + 5 \\ &= 2(x - 1)^2 + 3. \end{aligned}
後はCase 1と同様にして、頂点の座標は (1, 3) となります。
別の例も見て変形過程を確認しましょう。
Example 2
y = 3x^2 + 6x - 1
- 3x^2 + 6x の部分に注目する。
- 3(x^2 + 2x) のように x^2 の項の係数でくくる。
- 3(x^2 + 2x) = 3(x + 1)^2 - 3 のように変形する。
- y = 3(x + 1)^2 - 3 - 1 = 3(x + 1)^2 - 4 となり、頂点の座標は (-1, 4) となる。
式全体の変形は以下を参照してください。
\begin{aligned} 3x^2 + 6x - 1 &= 3(x^2 + 2x) - 1 \\ &= 3((x + 1)^2 - 1) - 1 \\ &= 3(x + 1)^2 - 3 - 1 \\ &= 3(x + 1)^2 - 4. \end{aligned}
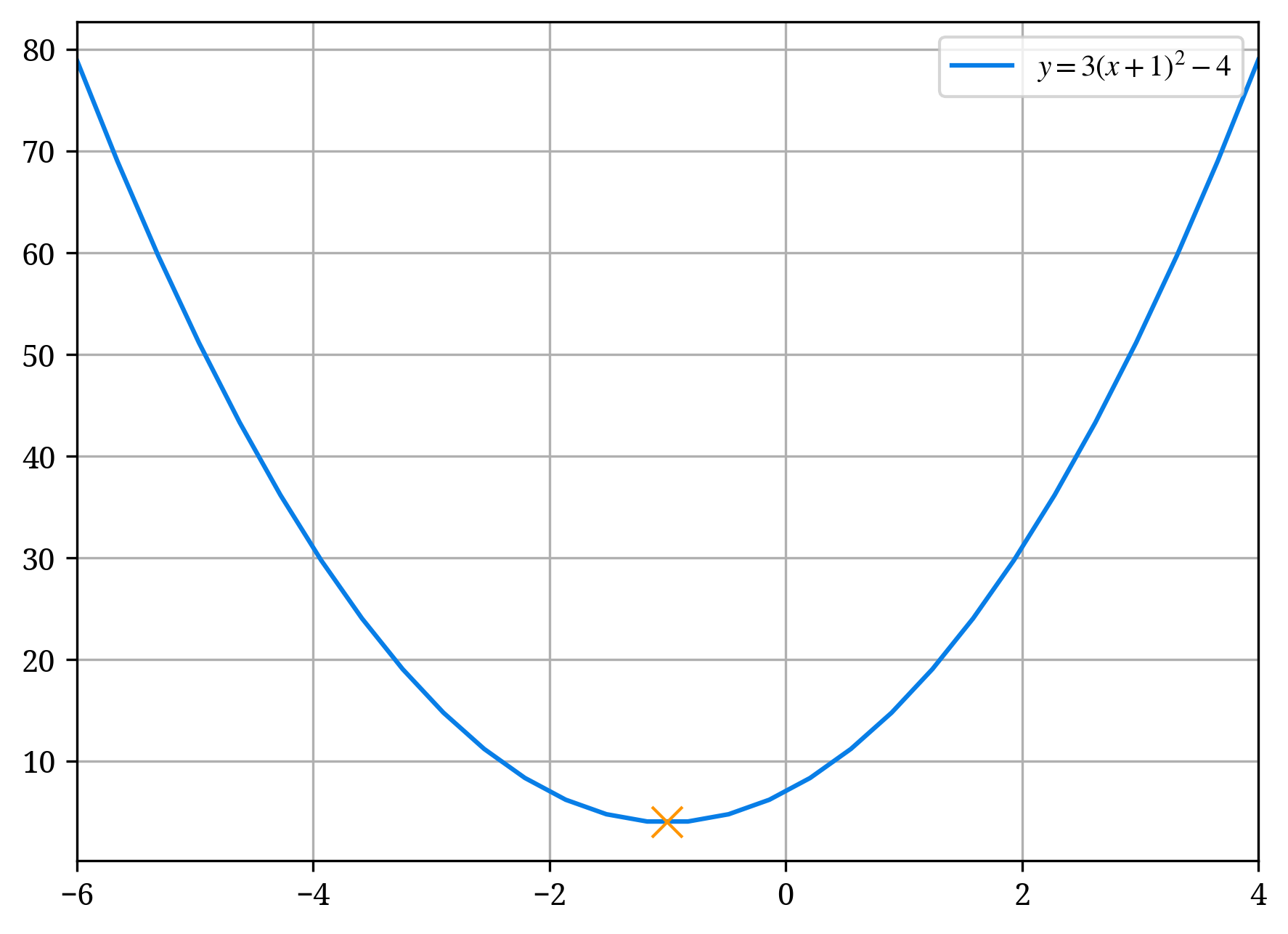
複雑な計算ですので、 慣れるまで練習を行ってください。なお、y = ax^2 + bx + c で与えられる二次関数の頂点の座標は一般的には以下のようになります。
\begin{aligned} y &= ax^2 + bx + c \\ &= a \left( x + \frac{b}{2a} \right)^2 - \frac{b^2 - 4ac}{4a}. \end{aligned}
したがって頂点の座標は
\left( -\frac{b}{2a}, - \frac{b^2 - 4ac}{4a} \right).
応用問題も解けることを目指す方は、上式のように一般的な係数についても頂点の座標を導出できるようになっておきましょう。
4 まとめ
結論として、二次関数のグラフである放物線は、自然界や様々な応用分野において重要な役割を果たしています。その頂点は、様々な現象を理解する観点から見ても重要な概念です。この記事では、放物線の特徴である頂点を求める手順を紹介しました。さらなる発展内容の基礎を作っていきましょう。









