三角関数の公式の公式をまとめています。本記事では公式を以下の2つのグループに分類しています。
- 三角関数の定義を使って証明されるグループ
- 加法定理を使って証明されるグループ
この分類は、後々、公式の証明方法を思い出す際に役立ちます。
1 三角関数の定義
三角関数には主にサイン(sin)、コサイン(cos)、タンジェント(tan)の3つがあります。Figure 1 に示した円の半径 r と円周上の点 A(x, y) の座標を使うと、三角関数は Definition 1 のように定義されます。
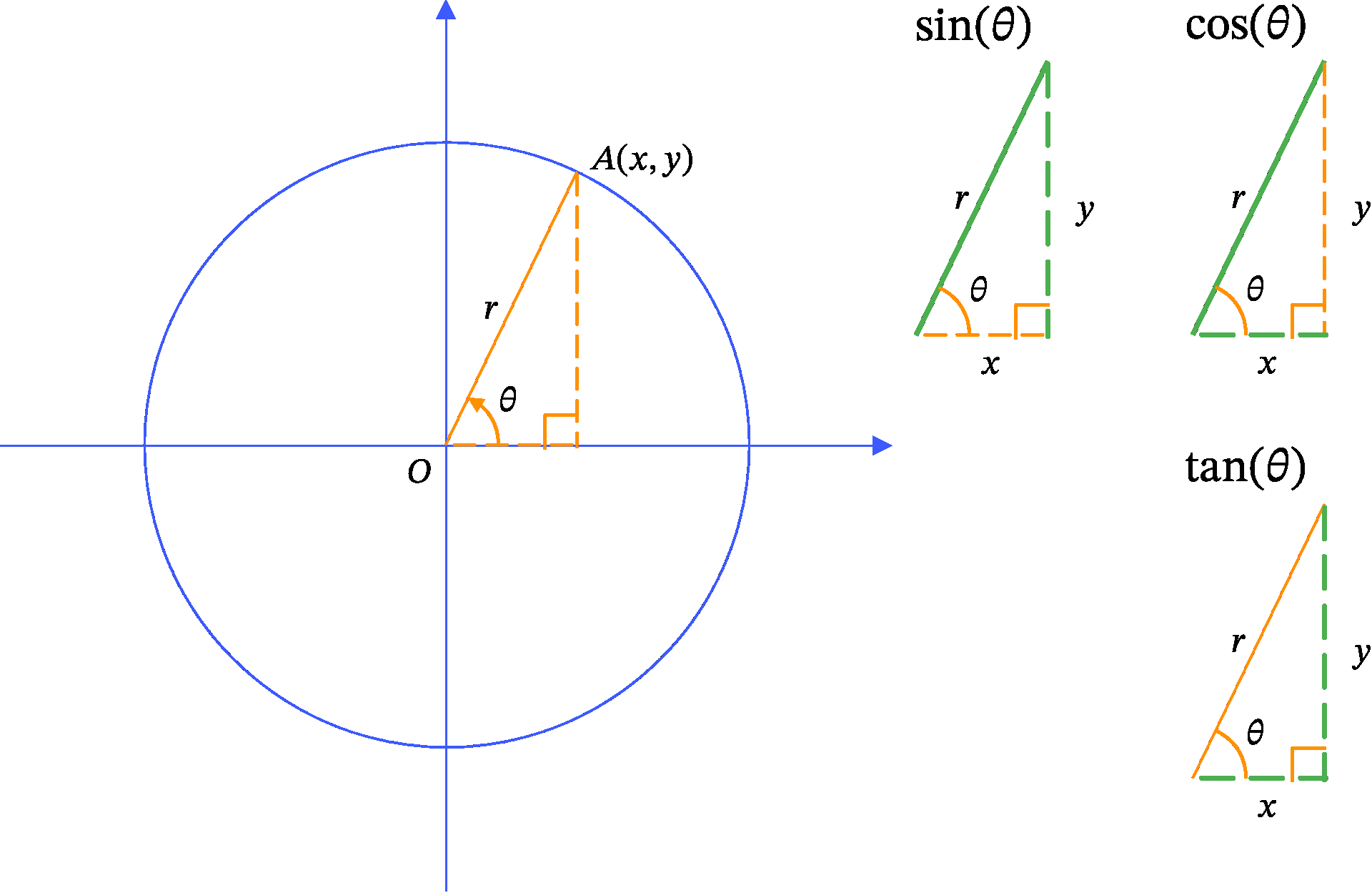
Definition 1 (三角関数の定義) \begin{aligned} \sin(\theta) &= \frac{y}{r}\\ \cos(\theta) &= \frac{x}{r}\\ \tan(\theta) &= \frac{y}{x} \end{aligned}
この定義が、三角関数全体の基本になります。
2 定義から証明する公式
三角関数の定義から証明される公式についてまとめておきます。
\sin^2{\theta} + \cos^2{\theta} = 1 \tag{1}
\tan(\theta) = \frac{\sin{\theta}}{\cos{\theta}} \tag{2}
1 + \tan^2{\theta} = \frac{1}{\cos^2{\theta}} \tag{3}
\sin{(-\theta)} = -\sin{\theta} \tag{4}
\cos{(-\theta)} = \cos{\theta} \tag{5}
\tan{(-\theta)} = -\tan{\theta} \tag{6}
\sin{(\pi - \theta)} = \sin{\theta} \tag{7}
\cos{(\pi - \theta)} = -\cos{\theta} \tag{8}
\tan{(\pi - \theta)} = -\tan{\theta} \tag{9}
\sin{\left(\frac{\pi}{2} - \theta \right)} = \cos{\theta} \tag{10}
\cos{\left(\frac{\pi}{2} - \theta \right)} = \sin{\theta} \tag{11}
\tan{\left(\frac{\pi}{2} - \theta \right)} = \frac{1}{\tan{\theta}} \tag{12}
3 加法定理
加法定理は、異なる角度を持つ三角関数を結びつけるための重要なツールです。具体的には以下のようになります:
Theorem 1 (加法定理)
- \sin(A + B) = \sin A \cos B + \cos A \sin B
- \cos(A + B) = \cos A \cos B - \sin A \sin B
- \tan(A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B}
角度が A-B の場合も加法定理としてよく記載しますが、Theorem 1 において B を -B で置き換えればすぐに証明できますので、ここでは省略します。
加法定理は三角関数の定義と並んで、他の公式を導くための基盤になります。加法定理自体は覚えておきましょう。
4 加法定理から導出する公式
これらの公式は加法定理を使って求めることができます。
2倍角の公式
\sin{2\theta} = 2\sin\theta \cos\theta \tag{13}
\cos{2\theta} = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2\sin^2\theta \tag{14}
\tan{2\theta} = \frac{2\tan\theta}{1 - \tan^2\theta} \quad (1 - \tan^2θ \neq 0) \tag{15}
半角の公式
\sin ^{2}\dfrac{\alpha }{2}=\frac{1 - \cos \alpha }{2} \tag{16}
\cos ^{2}\dfrac{\alpha }{2}=\dfrac{1+\cos \alpha }{2} \tag{17}
\tan ^{2}\dfrac{\alpha }{2}=\dfrac{1-\cos \alpha }{1+\cos \alpha } \tag{18}
三角関数の合成
a\sin \theta + b\cos \theta =\sqrt{a^{2}+b^{2}} \sin \left( \theta +\alpha \right) \tag{19}
ここで、
\begin{aligned} \cos \alpha &= \dfrac{a}{\sqrt{a^{2}+b^{2}}},\\ \sin \alpha &= \dfrac{b}{\sqrt{a^{2}+b^{2}}}. \end{aligned}
5 公式の覚え方よりも、理解が大事
公式は、できれば覚えてしまった方が便利ですが、理解せずに丸暗記することはお勧めしません。三角関数の公式の証明には、この分野で重要な式の変形や考え方が含まれており、単なる暗記よりも理解が重要です。
たしかに、試験に向けて公式はある程度覚えてしまった方が良いです。しかし、公式は何度も使っていれば自然と覚えてくるものです。問題を解いていても覚えられない、という方は、たぶん演習量が足りていないです。丸暗記に頼らず、公式を自然と覚えるくらいに問題演習をやってみてください。
結論として、“繰り返し証明を行い公式を理解しつつ、問題演習を通して自然と公式を覚える”、という流れをお勧めします。









