足して 180^\circ (\pi) になる角を”補角”と言います。三角関数の公式には、補角に関する公式がいくつかあります:
\sin{(\pi - \theta)} = \sin{\theta} \tag{1}
\cos{(\pi - \theta)} = -\cos{\theta} \tag{2}
\tan{(\pi - \theta)} = -\tan{\theta} \tag{3}
この記事では、これらの公式の証明を行います。三角関数には多くの公式が存在しますが、ほとんどの公式は簡単に導き出すことができ、覚えておく必要はありません。
1 証明のための基本的な考え方
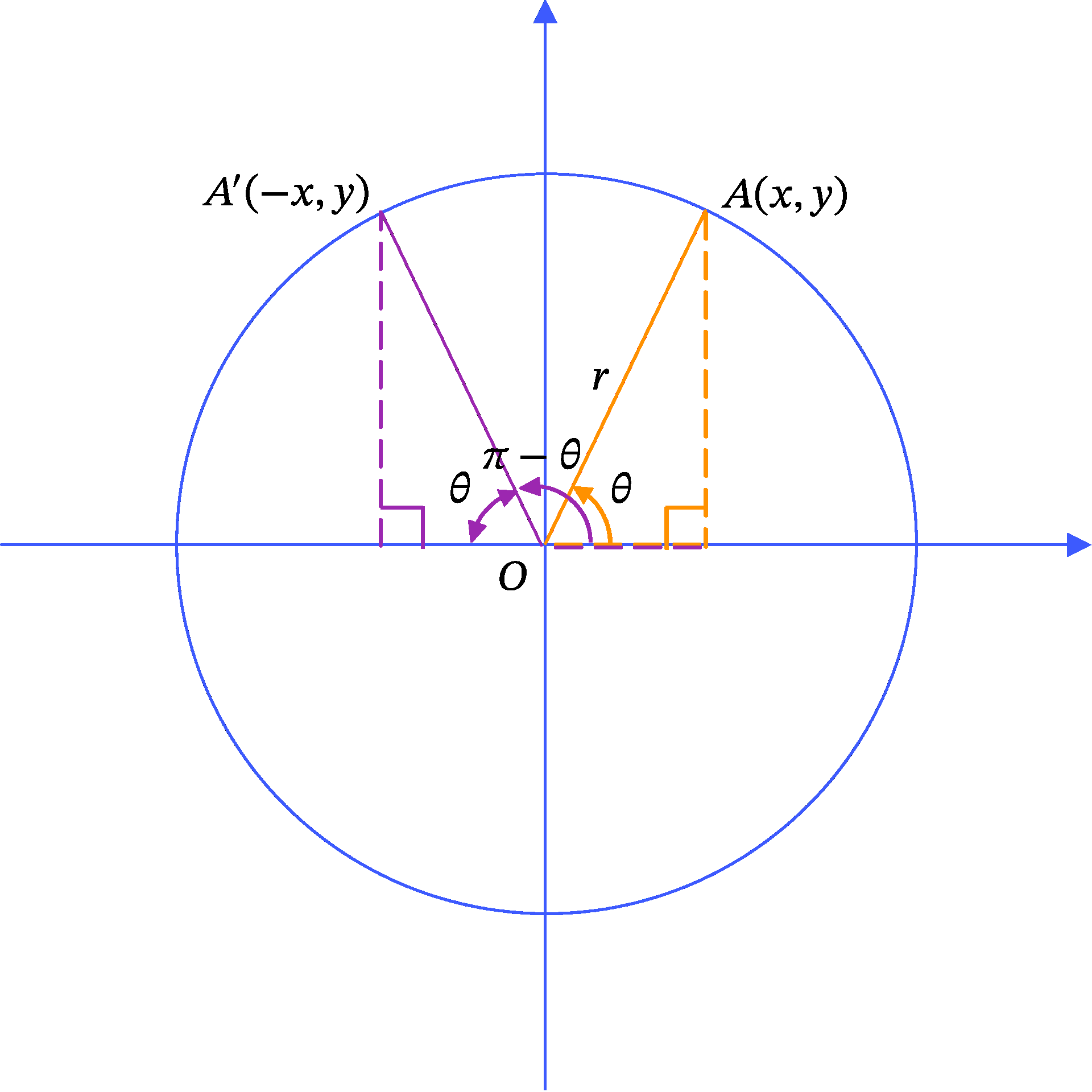
Equation 2, Equation 2, Equation 3 の証明では、Figure 1 が重要になります。
この図では、\pi - \theta は、一旦、 \pi だけ反時計回りに回転し、その後 \theta だけ時計回りに戻ると得られます。すると、Figure 1 の紫の直角三角形の中に \theta が現れます。このことから、点 A と 点 A' は、y 軸に関して対称な点であることがわかります。したがって、点 A の座標を (x, y) とすれば、点 A' の座標は (-x, y) となります。
Equation 2, Equation 2, Equation 3 は、\pi - \theta と \theta の関係を表しています。Figure 1 において、 \pi - \theta は点 A' に、 \theta は点 A にそれぞれ対応しています。したがって、これらの点に対してそれぞれ三角関数を表し、等しいことを確認すればよさそうです。
また、証明では三角関数の定義を用いますので、適時確認してください。
2 \sin{(\pi - \theta)} = \sin{\theta} (Equation 1) の証明
では、Section 1 の考えに従って、Equation 1 を証明してみましょう。まずは点 A' に注目します。三角関数の定義より、以下が成立します:
\sin (\pi - \theta) = \frac{y}{r}. \tag{4}
次に、点 A について三角関数の定義を適用してみましょう:
\sin \theta = \frac{y}{r}. \tag{5}
Equation 4 と Equation 5 より、
\sin (\pi - \theta) = \sin \theta
であることがわかります。ここでは、Figure 1 のように \theta が鋭角である場合を扱いましたが、同様のことが任意の \theta について成り立ちます。
これで Equation 1 を証明できました。
3 \cos{(\pi - \theta)} = -\cos{\theta} (Equation 2) の証明
Equation 1 と同様に、点 A、 A' それぞれに対して、三角関数の定義を適用します。点 A' の座標より:
\cos (\pi - \theta) = \frac{-x}{r} = - \frac{x}{r}.
ここで、点 A' の x 座標は -x で表されることに注意してください。
同様に点 A の座標から、
\cos \theta = \frac{x}{r}.
以上より、
\cos (\pi - \theta) = - \cos \theta
が成立します。
4 \tan{(\pi - \theta)} = -\tan{\theta} (Equation 3)
これまでと同様に、点 A'、点 A に対してそれぞれ三角関数を考えます。
点 A' について、x \ne 0 のとき、
\tan (\pi - \theta) = \frac{y}{-x} = - \frac{y}{x}.
x = 0 の時は タンジェントが定義されない点に注意してください。
同様に点 A について、
\tan \theta = \frac{y}{x}.
したがって、
\tan (\pi - \theta) = - \tan \theta
が成立します。
5 まとめ
三角関数における補角の公式の証明を行いました。足して 180^\circ (\pi) になる角は補角と呼ばれます。これらの公式は、三角関数の定義を使うと簡単に証明することができ、公式を丸暗記する必要はありません。三角関数の定義に使う円を描いて、公式を証明する手順に慣れておきましょう。









