「データを有効に使いたいけれど、何をすればいいかわからない」。そのお悩みはもっともです。記述統計学は基本的でありながら、データの特徴を知り、現状の理解や今後の方針を決める上で強力なツールとなりえます。本記事では統計学の基本として、記述統計学とは何か、なぜそれが重要なのか、推測統計学との比較、そして記述統計学にはどのような方法があるかを具体例を用いて解説します。記述統計学を使ってデータから意味のある情報を入手する方法を知り、役立てましょう。
1 記述統計学とは
そもそも統計学とは大雑把に言って、次のようにまとめられます。
「適切なデータを入手し、そのデータ自体やそのデータの元となる集団の特徴を調べること。またそのデータをもとに、未来の状態について推測すること。」
とりあえずは上記のように理解しておけばよいと思います。記述統計学(descriptive statistics)は統計量と呼ばれる数値やグラフなどを使って、手持ちの「データそのもの」について調べる統計学のことです。手持ちのデータそのものを調べるとはどういう意味でしょうか?ちょっと例を見てみましょう。
1.1 記述統計学の例
さて家庭菜園でキュウリが取れました (Figure 1) 。うちの今年のキュウリ1本は、だいたいどのくらいの質量なのでしょうか?とれたキュウリの質量を測って、平均を計算すればよさそうですね。

仮に1本1本、今年とれたキュウリの質量を測ると、以下のようなデータ (単位は g) が得られたとします。実際のデータを参考にしていますが、あくまでも説明用の参考値です。
284, 529, 255, 347, 280, 516, 147, 305, 341, 407, 429, 327, 508,
407, 730, 133, 453, 203, 240, 657, 621, 81, 326, 350, 40, 352,
419, 392, 60, 526Mean: 355.5このデータを眺めていても、キュウリの質量がおおよそどのくらいかはわかりません。そこで平均を計算して見ましょう。すると、おおよそ356 g となりました。ばらつきはかなり大きいですが、うちの家庭菜園の平均的なキュウリを1本収穫すると、だいたいこのくらいの質量に近いと言えそうです。
この例を振り返ってみると、調べる対象はうちの家庭菜園のキュウリ全体です。キュウリを収穫したら質量を測定すればいいので、とれたキュウリ全体について調査することができます。
これは全数調査 (census) と呼ばれ、調べたい全ての対象について調査することをいいます。記述統計学はこの全数調査を基本とします。今回の例では調べたい対象全体である、うちでとれたキュウリについて平均をもとめました。これが Section 1 でご説明した、“データそのものを調べる”という意味です。さらに理解を深めるため、記述統計学と推測統計学を比較してみましょう。
1.2 記述統計学と推測統計学の比較
推測統計学 (inferential statistics) では記述統計学とは異なり、手持ちのデータそのものを調べたいわけではありません。調べたいのは、データの背後にある母集団 (population) と呼ばれる集団の特徴です。これはどういう意味なのか、例を見てみましょう。
例えば日本で収穫されたキュウリの質量の平均値を知りたいとします。「先ほどの家庭菜園でとれたキュウリの質量の平均が356 g だから、だいたいそのくらいでは?」、と思う方もいらっしゃるかもしれませんが、実のところそうはいかないのです。キュウリは一気に生長することもあり、収穫し忘れているとあっという間に巨大になってしまいます。うちのキュウリも巨大になっていることがよくあり、これではかなり偏ったデータになってしまいます。
したがって、個人の家庭菜園ではなく日本で収穫されたキュウリについて調べる必要があるのですが、これまた家庭菜園と同様には調べられません。先ほどの家庭菜園の例では、収穫したキュウリすべての質量を測ることは不可能ではありません。一方で日本で収穫されたキュウリ全ての質量を測定して、その平均を求めることは不可能といっていいでしょう。あまりに数が多すぎます。
日本のキュウリ全体を調べることができない中で、どうやって日本で収穫されたキュウリの質量の平均を調べればよいのでしょうか?実際の値は誰にもわかりませんが、それらしい値を推測することは可能です。まず、できるだけ母集団 (日本で収穫されたキュウリ) の構成に近い (と思われる) キュウリを、ある程度の数、何らかの方法で抽出します。これを日本のキュウリの代表とします。これらキュウリの集団をサンプルとよび、その平均から、「母集団である日本にあるキュウリ全て」、の平均的な質量を調べ推測します。
先ほどの家庭菜園の例と同様、サンプルに偏りがあると母集団の平均をうまく推測できません。やたらと重いキュウリばかり集めてそれをサンプルにすれば、当然ながらそのサンプルを使って推測した母集団の平均値は、本来の母集団の平均値よりも大きくなっているはずです。
このように推測統計学では全数調査ができない対象に対して、サンプルを用いてその母集団の特徴を調べることが行われます。しかしながら、記述統計学と推測統計学では調べる対象に対して大きな違いがある一方、推測統計学でも記述統計学で行うような統計量の計算やグラフの作成を最初に行います。この意味で推測統計学は記述統計学をベースにしています。したがって母集団について知りたい場合も、記述統計学の知識が大きく役立ちます。
2 記述統計学を使ってデータから意味のある情報を得る方法
ではデータそのものについて調べる記述統計学には、どのような方法があるのでしょうか?
データの種類にもよりますが、データは端的に言って数値の集まりです。図や表などに加工していない元々のデータを生データ(raw data)と呼びます。この生データそのものを見ていても、データの特徴はわかりません。例えば以下の数値を見てください。
207.9, 282.1, 403.4, 424.4, 572.5, 361.7, 374.5, 332.3, 309.4, 428.2, 385.3, 329.3, 242.,
337.7, 310.9, 475.5, 444.7, 247.8, 466.7, 292.8, 363.3, 470.3, 247.5, 366.,
237., 155.9,
448.7, 352.8, 267.8, 191.3何かデータの特徴はわかりますか?このような数値の並びを見てもなかなか特徴は見えてきません。記述統計学ではこのようなデータに対して主に2通りの方法によりデータを要約します。
- 統計量の計算(定量的に調べられる)
- 表やグラフの作成(視覚的に見やすい)
統計量と呼ばれる数値を計算すると、数値としてデータを要約することができます。数値ですので他のデータと比較を行いやすくなります。一方、表やグラフを使うとデータを視覚的に把握しやすくなります。統計量だけでは見えづらいデータの全体的な傾向も把握することができます。どちらか、ではなくどちらの方法も重要です。
以降では代表的な統計量と図表について簡単にご紹介します。
2.1 統計量を使ったデータの整理
主な統計量 (statistic) には以下の3つの種類があります。
- 代表値と呼ばれるデータの分布の中心を表す指標(平均値や中央値)
- データのばらつきを表す指標(範囲、標準偏差、四分位範囲)
- データの分布の形を表す指標(歪度)
2.1.1 代表値
データは常に同じ値が得られるわけではなく、何らかの分布に従って存在していると考えることができます(Figure 2)。
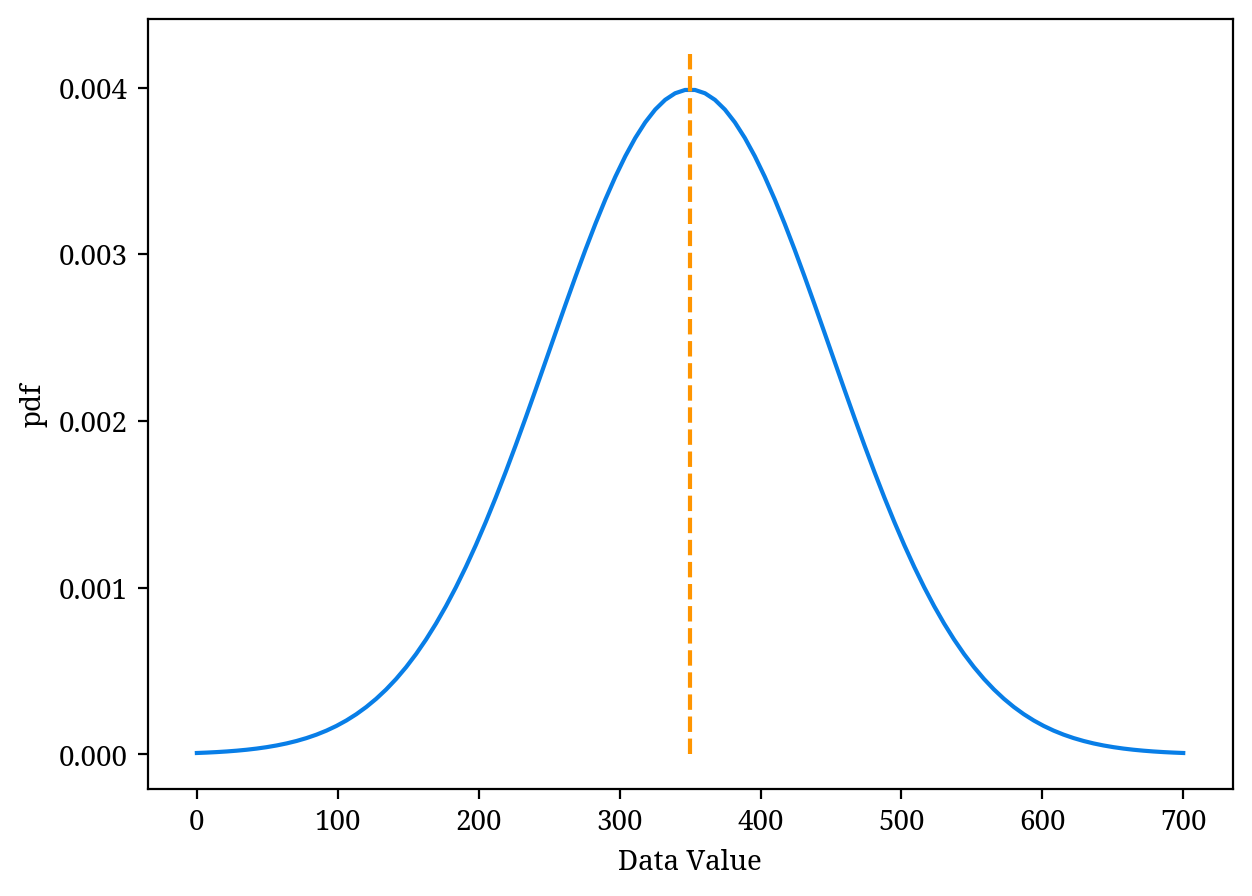
各データの値(Data Value)とそれぞれの頻度を表す。オレンジの破線:分布の平均値。
代表値はデータがどのような値の周辺に存在するかを表しています。平均値や中央値がこのグループに含まれます。データによって平均値で問題ない場合や中央値の方が適する場合もあり、使い分けが重要です。例えば下記の記事では平均と中央値の違いについて解説しています。
2.1.2 データのばらつきを表す指標
代表値が同じ値であっても、データの分布の様子はかなり異なる場合があります。データが代表値の周辺に集まっているのか、それとも広く分布しているかは「データのばらつきを表す統計量」で定量化できます。このグループには範囲、標準偏差、四分位範囲などが含まれます。
分散もデータを表す指標として紹介されますが、実際の解析では分散ではなく標準偏差を利用します:
なお標準偏差は平均値と、四分位範囲は中央値とセットで使われます。なぜ標準偏差は平均値と、四分位範囲は中央値とセットで使うのか、分散ではなく標準偏差を使う理由など、理解しておくことが望ましいです。
Figure 2 ではデータは左右対称に分布していますが、実際のデータは必ずしもそうとは限りません。Figure 3 のように左右対称ではない分布など、右(right-skewed distribution)または左(left-skewed distribution)に歪んだ分布もあります。
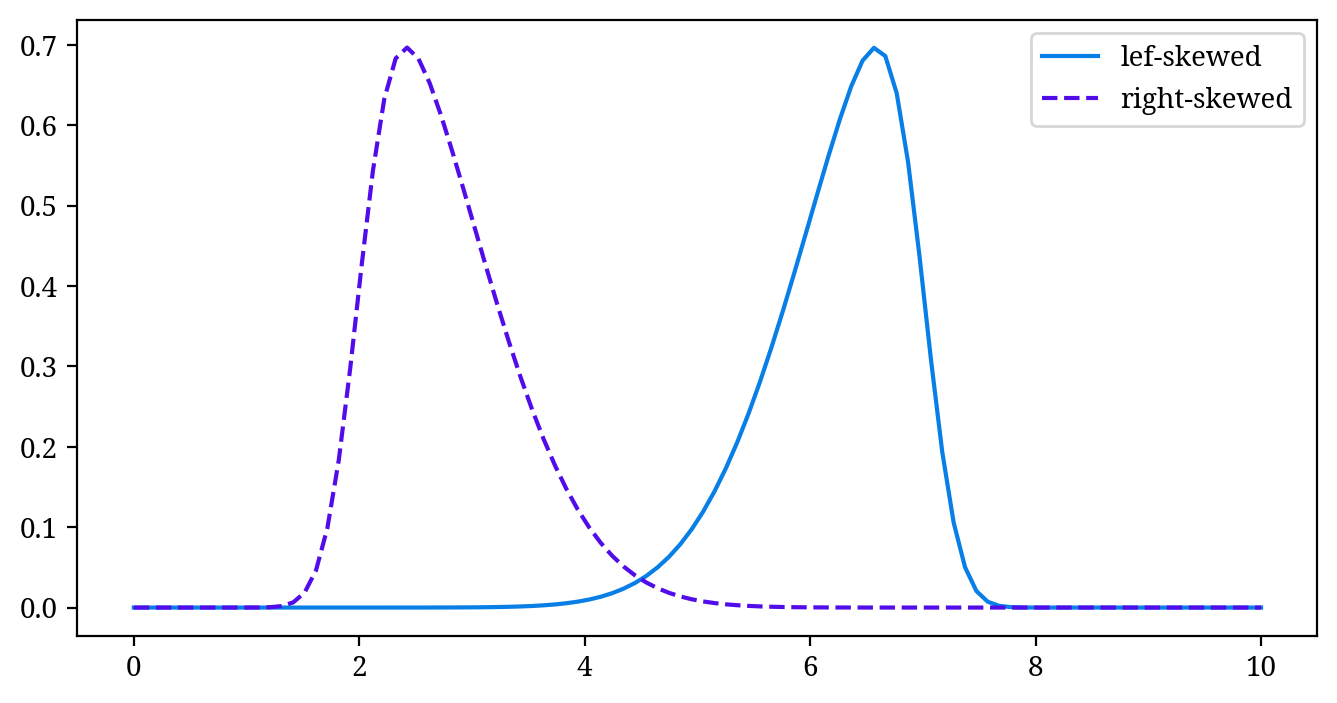
この歪み具合は歪度(ワイド)と呼ばれ、分布の形状についての統計量となります。
2.2 表やグラフを使ったデータの整理
ここでは代表的なグラフを紹介します。
ヒストグラム
ヒストグラムはデータの分布を表します。横軸がデータの値、縦軸がそのデータの頻度を表します。もう少し正確に言うと、横軸にデータを表す際は、データを適当な幅で区切ります。縦軸はその幅の中に存在するデータの数を表しています(Figure 4)。
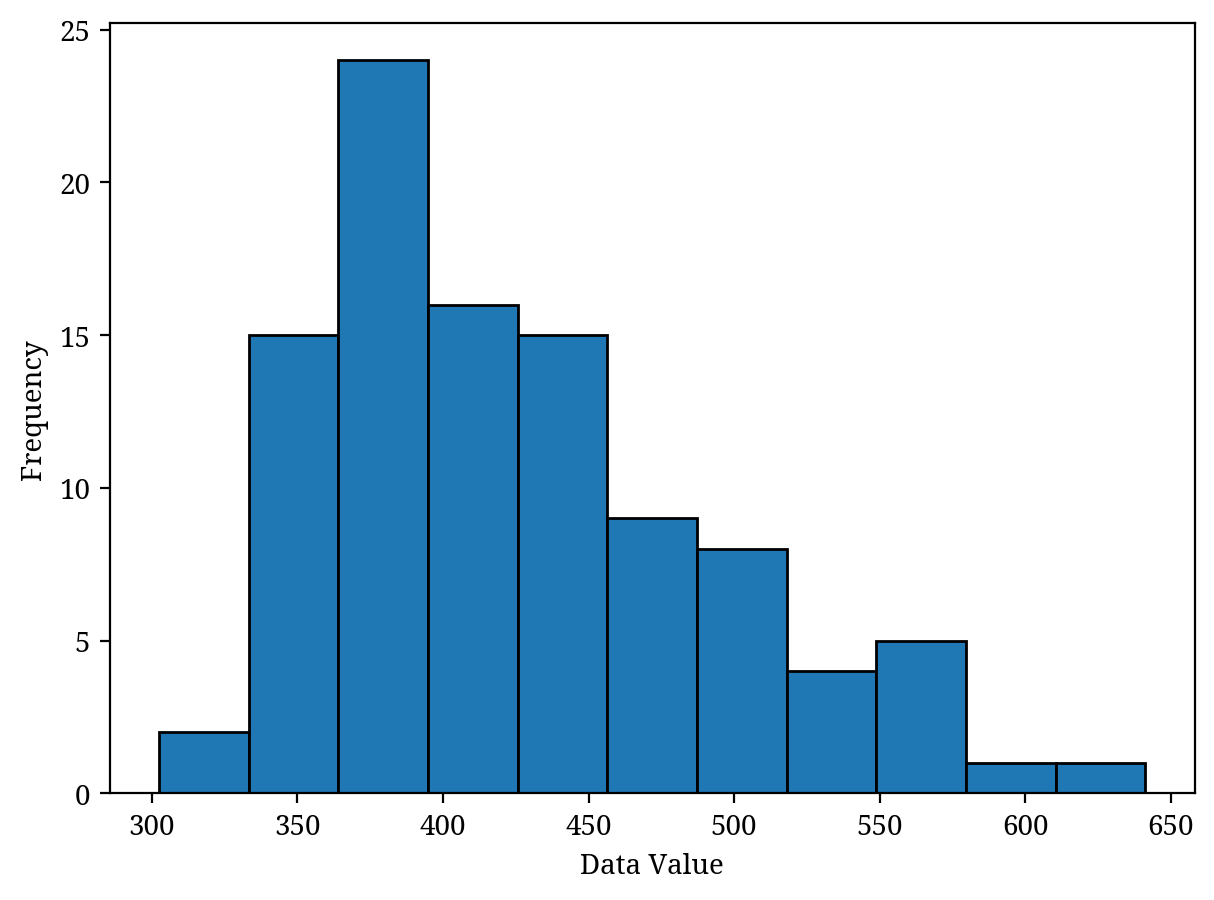
ヒストグラムは高度な解析手法を行う前に、大抵の場合必要です。まずはヒストグラムでデータの分布を把握し、必要に応じて適切な処理を行い、その後解析手法を適用します。このようにヒストグラムは非常に重要な図の一つです。
箱ひげ図
ヒストグラムはデータの分布を表す際に非常に良いのですが、複数の分布を比較する際は必ずしも視覚的に理解しやすいわけではありません。
複数のデータを比較する場合は、ヒストグラムの代わりに箱ひげ図を使うと良いです。箱ひげ図はデータの分布の中心(代表値)、データのばらつき、そして外れ値など様々な情報をまとめて表示することのできる非常に優れた図です (Figure 5 (b))。
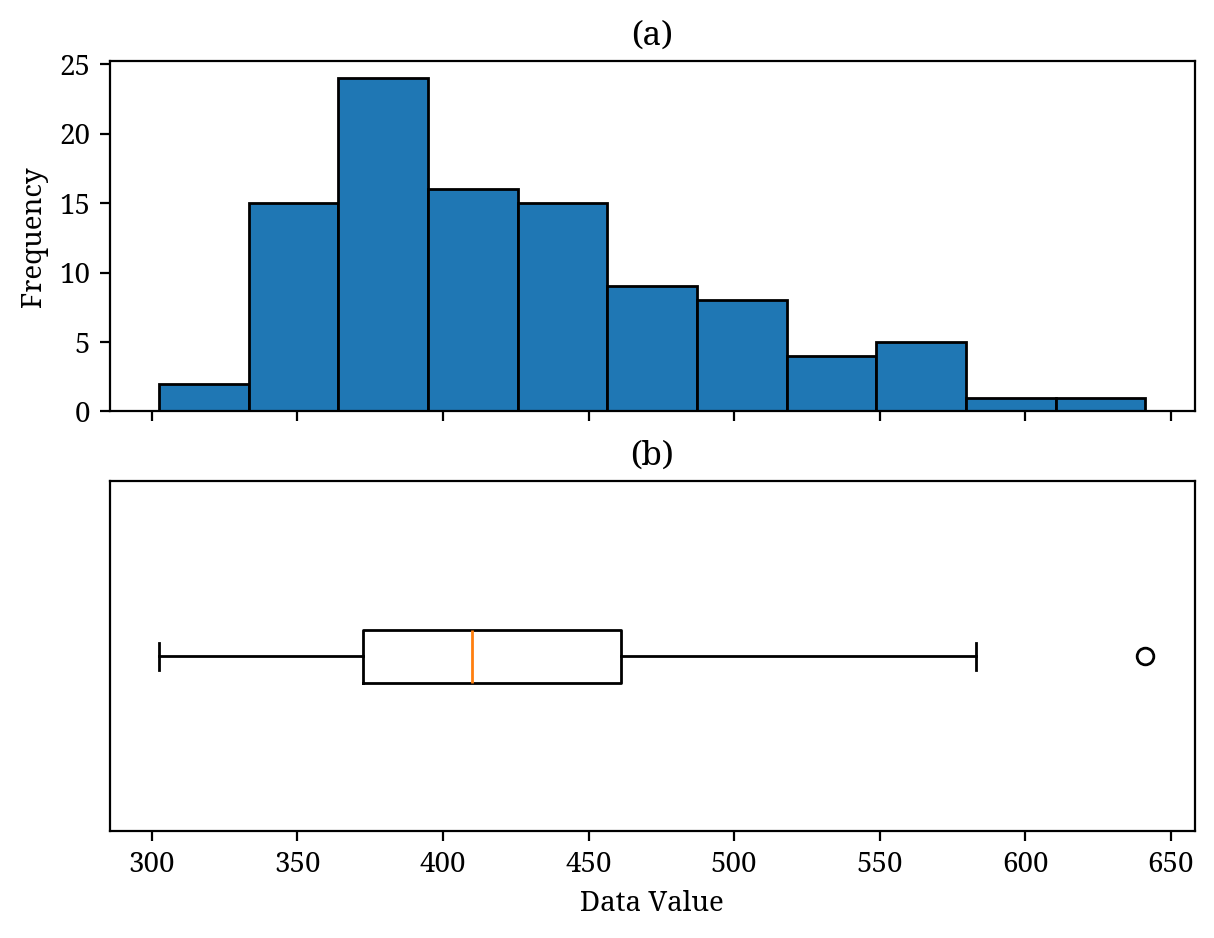
箱ひげ図 (b) はヒストグラム (a) の要約である。(b) オレンジの線: 中央値。白丸: 外れ値。
箱ひげ図はヒストグラムを要約した図です。したがって Figure 5 のようにヒストグラム (a) と箱ひげ図 (b) を対応させることができます(Figure 5 は学習用にヒストグラムと箱ひげ図を同時に表示していますが、通常は目的に応じてどちらかを使います)。
Figure 5 (b) ではオレンジの線が「中央値」を表し、箱の横方向の長さが「四分位範囲」(ばらつき)を表しています。詳細は省略しますが、箱の横にある黒線は通常データの「最小値」(左)と「最大値」(右)を表します。白丸は外れ値(他のデータの値とは大きく乖離した値)です。今回は外れ値が見られるので、右側の黒線はデータの最大値を表しているわけではありません。
箱ひげ図は多くの情報を一度に表示ができるうえ、複数のデータセットの比較も行いやすい非常に優れた図ですが、最初は見方がわからないかもしれません。箱ひげ図の見方については下記の記事で解説しています:
箱ひげ図は外れ値を見つける際にも役に立ちます (Figure 5 (b) の白丸)。外れ値について検討せずに解析を進めてしまうとデータの特徴を正確に把握できなくなってしまったり、その後の解析で余計な手間が増えてしまうかもしれません。箱ひげ図を使えば視覚的に外れ値を把握することができます。このような使い方もぜひ覚えておきましょう:
箱ひげ図自体はヒストグラムを要約した図ですので、箱ひげ図からヒストグラム(データの分布)を想像できるようになることが大事です。
棒グラフ
棒グラフはよく見る図かもしれません。一見するとヒストグラム (Figure 4) と棒グラフ (Figure 6) は似ているように見えるかもしれませんが、実際は全く別のグラフです。ヒストグラムでは横軸に連続的なデータ(実数)を表示しますが、棒グラフではGroup A、Group Bのようなカテゴリを表します。
今回は記述統計学の文脈なので描いていませんが、母集団の平均値を推測したい場合は、棒グラフに「エラーバー」を表示します。
散布図
1人の人について「身長」と「体重」のデータがある場合など、1つのデータポイント(調査した1つ1つの対象)に2つのデータが存在する場合は、散布図 (Figure 7) を作成すると、2つのデータ間の関係が見やすくなります。
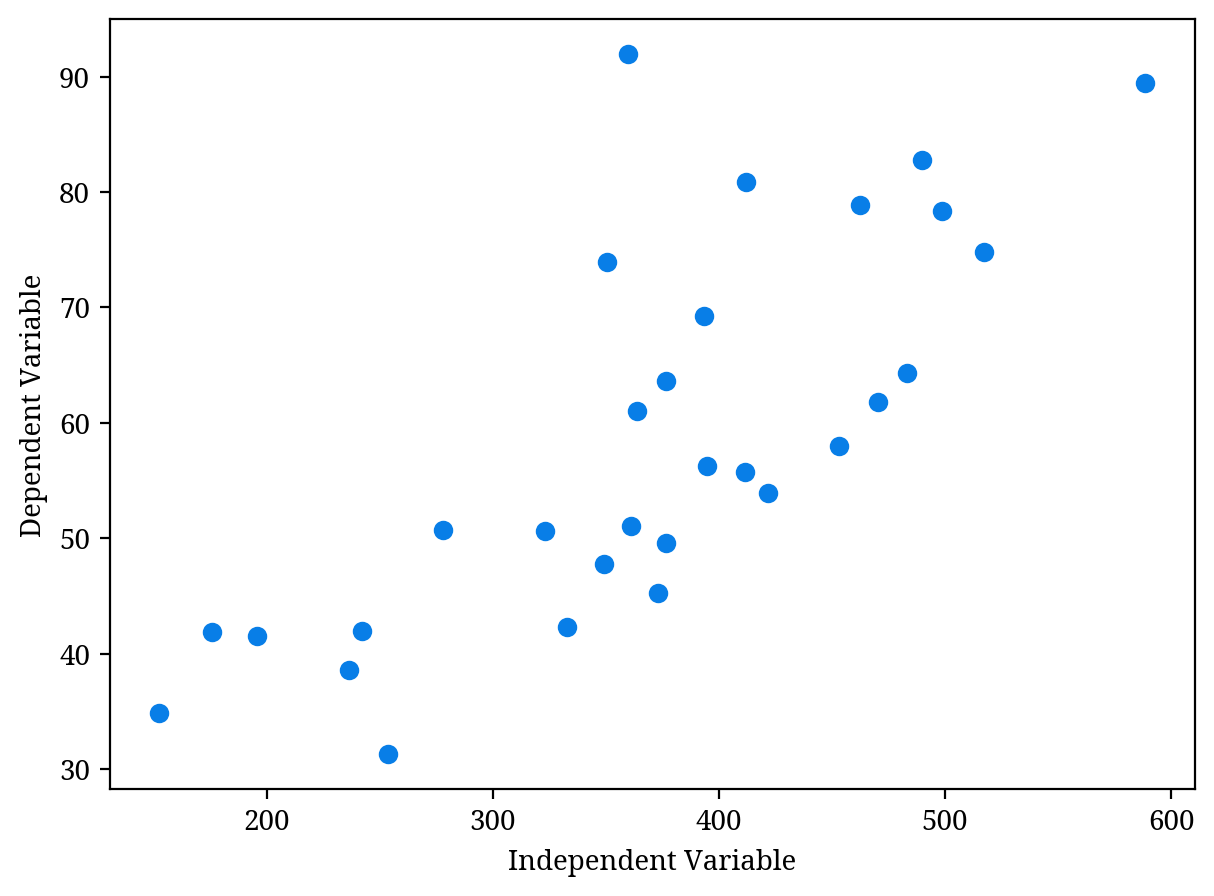
散布図上の各点は xy-平面上の点のように描きこむことができます。下記の記事では散布図の構造や散布図の見方について解説しています。
散布図を基に2つのデータ間の関係を視覚化した後は、相関係数を求めたり、回帰分析を行うこともあります。
- 相関係数: 2つのデータが連動しているかを定量化した値
- 回帰分析: 将来新しく独立変数 (independent variable) が得られたとき、従属変数 (dependent variable) の値を予測する手法。
相関係数は -1 から 1 の値をとり、2つのデータが連動する程度やその方向を表すことができます。例えば相関係数の値が -1 に近ければ、2つのデータは”強い負の相関”を示すと表現されます。逆に 1 に近ければ、“強い正の相関”を示しています。相関係数の値と相関の強さの目安については、下記の記事で解説しています。
相関係数を使って2つのデータの連動を数値化 (定量化) することはできますが、注意しなければならない点も多いです。例えば相関係数はあくまでもデータ間の直線的な連動を表します。どういう意味かというと、たとえばデータが放物線に沿って分布しているときは、相関係数の値は 0 に近くなってしまします。相関係数の値が 0 に近いと、その2つのデータは無相関であると判断されます。つまり連動していないということになります。実際には放物線に沿って連動しているにも関わらず、です。
こういった状況では相関係数を使うことは適切ではありません (Note 1)。 相関係数を計算する前に散布図を描いておくと、データの分布が直線的かどうか判断できますから、うっかり”無相関だ”と判断してしますリスクを減らせます。
散布図と相関係数の関係については以下の記事で解説していますので、ぜひ読んでみてください:
NOTE 1: 単に”相関係数”というときは
より正確には”Pearson’s r”のことです。ふつう”相関係数”という場合は、この”Pearson’s r”のことを言います。相関を表す指標は他にもあり、散布図上のデータの分布が直線的ではないとき (“非線形”と言います) は、それらの指標を使う必要があります。
3 統計量の計算やグラフを作成するためのツール
統計量の計算やグラフの作成は、ツールを使うことで簡単に行えます。これらのツールには、主に2つのカテゴリがあります。1つは表計算ソフト、もう1つはプログラミング言語です。それぞれの特徴を見ていきましょう。
3.1 表計算ソフト
表計算ソフトは、データを整理し、視覚的に分析するための直感的なツールです。これらのソフトでは、数値データをセルと呼ばれる枠に入力し、簡単な数式や関数を使って統計量を計算できます。また、グラフ作成機能も備わっており、データの視覚化もできます。操作が簡単でありながら、多くの基本的な統計分析が可能なので、初心者にも扱いやすいです。
3.2 プログラミング言語
一方でプログラミング言語を使うこともできます。初心者には特に”Python”言語がおすすめです。シンプルな文法と豊富なライブラリ(例:“pandas”, “NumPy”, “Matplotlib”など)のおかげで、データを分析しやすい形に整形したり抽出したりと、必要な処理を簡単に行えます。
目的によっては、グラフの細かい部分の編集や、表計算ソフトに備わっていないグラフを作成したいことがあるかもしれません。プログラミング言語ではこういったカスタマイズを柔軟に行うことができます。またデータ処理の自動化や再現性のある分析ができる点でも大きなメリットがあります (Note 2)。 表計算ソフトに比べると敷居は少し高いですが、スキルを身に着ける価値も大きいです。
NOTE 2: プログラミング言語を使った自動化や再現性
プログラミング言語では、一連のデータ処理の過程をテキストファイルとして作成します。ループ処理を行うコードを使えば、同様の処理を少し値を変えながら、繰り返し行うことができます。また専用のシステムを使い、テキストファイル内のコードの変更点を履歴として保存すると、処理の過程や変更点のチェックも簡単です。
3.3 表計算ソフトとプログラミング言語の使い分け
表計算ソフトとプログラミング言語は自分のニーズに応じて選ぶことが重要です。職場によっては表計算ソフトを利用が必要なこともあるでしょう。スキルアップのため、まずは表計算ソフトで基本的な操作に慣れ、その後”Python”言語に挑戦してみるのも良いでしょう。どちらのツールにもメリットデメリットがあります。目的やニーズ、自分のスキルレベルに応じて使い分けていきましょう。
4 まとめ
本記事ではデータを有効に使うため、記述統計学について解説しました。記述統計学では統計量や図を使ってデータを要約することができます。記述統計学を使えば、複雑な理論なしにデータについての様々な情報を得ることができます。これらのアプローチはデータの特徴を知ることに大きく役立ち、また推測統計学の基本にもなります。適切な統計量や図を使って、データに対する理解を深めていきましょう。









