三角関数の定義について解説しています。この定義は三角関数全体の基本ですので、しっかりと理解しておく必要があります。また定義を理解しておくと、\sin \left( \frac{\pi}{4} \right) など、三角関数の代表的な値について、覚えておく必要がなくなります。
1 三角関数の定義
三角関数には主にサイン(sin)、コサイン(cos)、タンジェント(tan)の3つがあります。これらはそもそもは直角三角形における辺の比率です。しかし直角三角形という前提があると角の大きさとして鋭角(0^\circ から 90^\circ)の場合しか扱えません。したがってより一般的な角度を扱うために、三角関数は円を使って定義されます (Figure 1)。
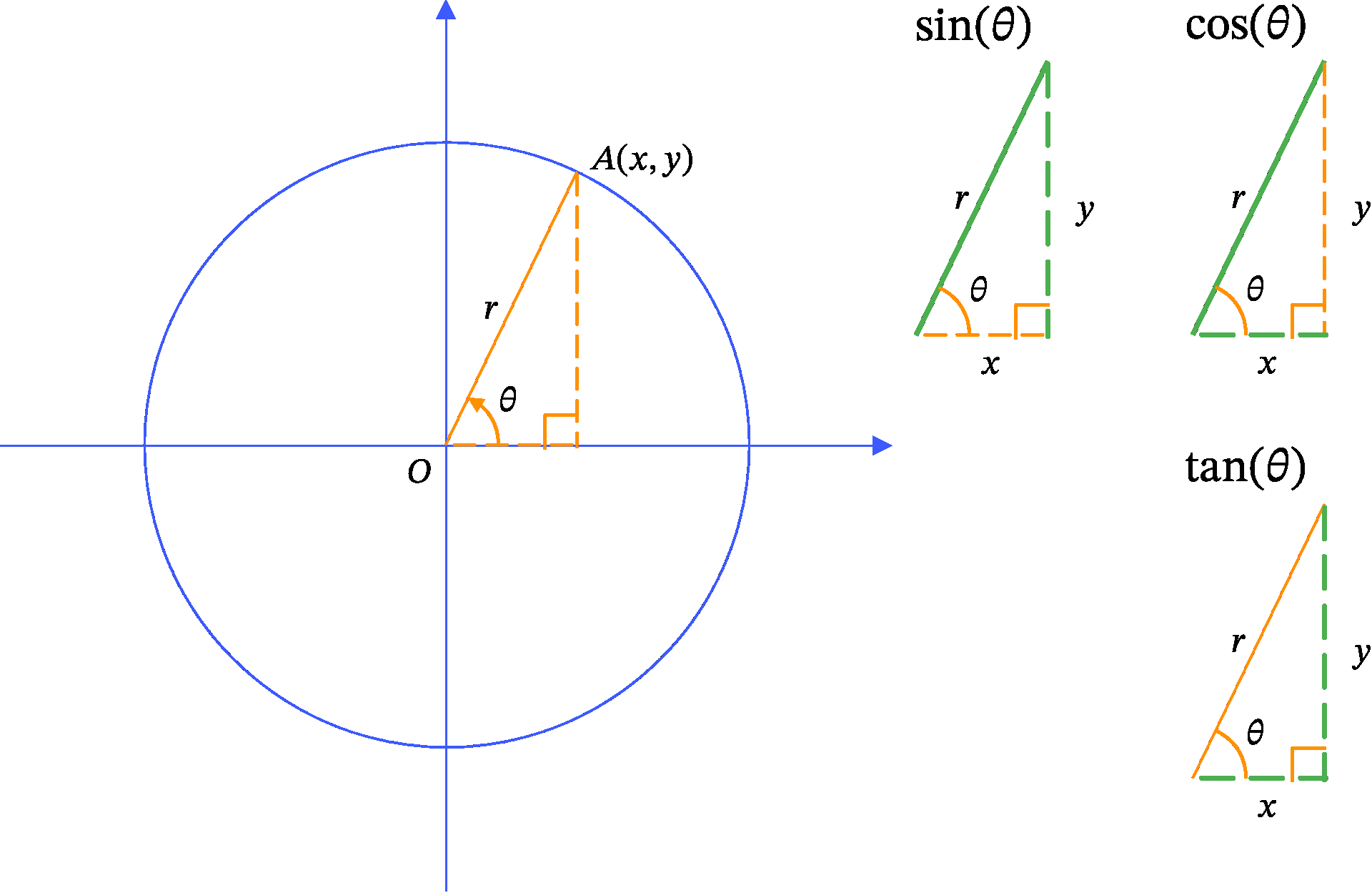
Figure 1 では以下のステップで円や点を作成しています。
- 中心が原点 O 、半径が r の円を描きます。
- この円周上に適当に点 A を加えます。この点 A の座標を (x, y) とします。
- 点 A と円の中心を端点とする線分 OA を描きます。
- x 軸と線分 OA の間の角を \theta とします。このとき \theta は、x 軸の正の方向から反時計回りに測った角です。
この r、x、y、\theta を組み合わせて三角関数を定義します:
Definition 1 (三角関数の定義) \begin{aligned} \sin \theta &= \frac{y}{r}\\ \cos \theta &= \frac{x}{r}\\ \tan \theta &= \frac{y}{x} \end{aligned}
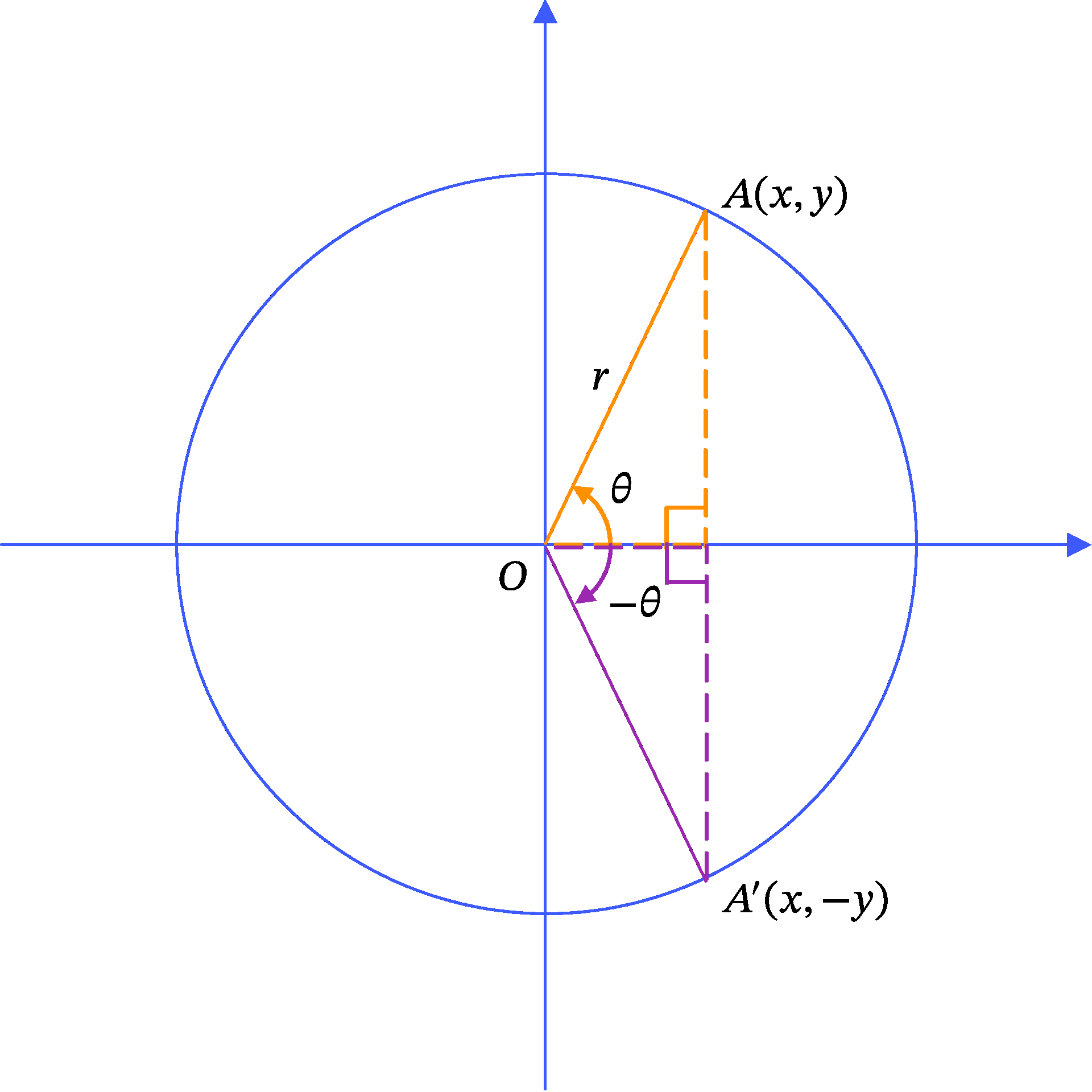
この定義では \theta を x 軸の正の方向から反時計回りに測るので、 \theta は 120^\circ や 360^\circ、それよりも大きい角度をもつことができます。また、逆に x 軸の正の方向から時計回りに角度を測ることもできます。反時計回りの場合を正の角度、時計回りの場合は負の角度と決めておきましょう。Figure 2 では、正の値を持つ角度 \theta は x 軸と線分 OA で決まり、負の値を持つ角度 -\theta は、 x 軸と線分 OA' で決まります。
2 x, y, \theta の関係
Definition 1 において、x, y, \theta の間には以下の式が成立します:
r^2 = x^2 + y^2 \Leftrightarrow r = \sqrt{x^2 + y^2}.
Figure 1 中の、オレンジの直角三角形について、三平方の定理を考えると、簡単に導けます。r > 0 ですから、r = \sqrt{x^2 + y^2} となることもわかります。
また、Definition 1 において、\sin \theta = \frac{y}{r} の両辺に r を掛けると、y = r \sin \theta が得られます。同様に \cos \theta = \frac{x}{r} ですので、 x = r \cos \theta となります:
\begin{aligned} x &= r \cos \theta,\\ y &= r \sin \theta. \end{aligned}
この式から、x 座標、 y 座標を、 r と \theta を使って表せることがわかります。極座標ではこのような見方が重要になってきます。
3 単位円を使った、三角関数の定義
Definition 1 では半径 r の円を用いました。テキストによっては、半径 r の代わりに、単位円を使うこともあります (単位円は、半径が 1 である円のことです)。実は三角関数の値は、円の半径に依存しないので、 Definition 1 のように任意の半径でも、半径 1 でも問題ありません。
4 定義を使った、三角関数の代表的な値の求め方
通常、三角関数の値を求める際は計算機が必要になりますが、角度によっては Definition 1 を使って簡単に三角関数の値を求めることができます。例えば、\theta = 0 の場合を考えてみましょう。


\theta = 0 のとき
Figure 3 (a) では半径 r の円を考えています。このとき、 \theta = 0 に対応する円周上の点は A(r, 0) となります。この座標と半径を、Definition 1 に代入して、三角関数の値を求めることができます。
\begin{aligned} \sin 0 &= \frac{y}{r} = \frac{0}{r} = 0, \\ \cos 0 &= \frac{x}{r} = \frac{r}{r} = 1, \\ \tan 0 &= \frac{0}{r} = 0. \end{aligned}
定義を使って、簡単に値を求めることができました。
\theta = \frac{\pi}{3} のとき
\theta = \frac{\pi}{3} のときも、三角関数の値を求めてみましょう。\theta = \frac{\pi}{3} のとき、 Figure 3 (b) の状況になります。 \frac{\pi}{3} = 60^\circ ですから、辺の比が 1 : 2: \sqrt{3} の直角三角形を考えることができます。
ここで、Section 3 においてお話ししたように、三角関数の値は半径に依存しません。言い換えると、任意の半径の円に対して三角関数を考えてよいことになります。今回は半径 r = 2 とすることで、\theta = \frac{\pi}{3} に対応する点 A の座標が (1, \sqrt{3}) であることがわかります。
したがって、以下のように三角関数の値を計算することができます:
\begin{aligned} \sin \frac{\pi}{3} &= \frac{y}{r} = \frac{\sqrt{3}}{2}, \\ \cos \frac{\pi}{3} &= \frac{x}{r} = \frac{1}{2}, \\ \tan \frac{\pi}{3} &= \frac{\sqrt{3}}{1} = \sqrt{3}. \end{aligned}
Tip 1: TIP: 定義を使った、三角関数の値の計算
定義における円の半径は、使いやすい値を使うことができる。
- \frac{\pi}{6}, \frac{\pi}{3}, \frac{2 \pi}{3}, \frac{5 \pi}{6} など: 半径 2
- \frac{\pi}{4}, \frac{3 \pi}{4} など: 半径 \sqrt{2}
今回は円の半径として 2 を使いましたが、 \frac{\pi}{4} などの場合は、直角二等辺三角形を考え、 \sqrt{2} を使うと良いでしょう。

このように三角関数の定義を使えば、三角関数の値を簡単に求めることができますので、値を覚えておく必要はありません。むしろ、定義を使って値を求める手順に慣れておきましょう。
5 三角関数の取りうる値の範囲
三角関数の定義 Definition 1 から、三角関数がとりうる値について知ることができます。
5.1 サインの取りうる値の範囲
まずサインは以下のように定義されました:
\sin \theta = \frac{y}{r}.
r は定数 (固定された値) ですから、円周上の点の y 座標によって、サインの値が決まります。直角三角形を使った三角比の定義では、各辺の値が正でしたので、三角比の値は常に正の値をとりました。一方、この定義では Figure 1 のように、 y 座標は正、負、 0 をとります。したがって、サインは正と負の値、そして 0 をとります。
では、サインはどんな正の値、負の値でもとることができるのでしょうか?ここでいう y 座標は、あくまでも Figure 1 に示した円周上の点の y 座標です。この図から、 y の値は -r \le y \le r であるとわかります。y は最大で半径 r の値を、最小でそのマイナスをとった値 -r をもつ、ということですね。
したがって、 \sin \theta = \frac{y}{r} は以下の範囲の値を持ちます:
\frac{-r}{r} \le \frac{y}{r} \le \frac{r}{r}.
以上より、 -1 \le \sin \theta \le 1 です。
5.2 コサインの取りうる値の範囲
コサインについてもサインと同様に考えることができます。コサインの定義は \cos \theta = \frac{x}{r} ですから、 x の値の範囲を考えましょう。Figure 1 より、
-r \le x \le r.
したがって、
\frac{-r}{r} \le \frac{x}{r} \le \frac{r}{r}.
以上より、 -1 \le \cos \theta \le 1 です。コサインはサインと同じ範囲の値をとることがわかります。
5.3 タンジェントの取りうる値の範囲
タンジェントはサイン、コサインと異なり、 \tan \theta = \frac{y}{x} ですから、サイン、コサインよりも複雑な考えが必要です。少し複雑ですので、ひとまず結論だけを述べると、タンジェントは任意の実数の値をとることができます。簡単に言うと、どんな大きな値も、小さな値もとることができます。
タンジェントの取りうる値の範囲について説明しますが、難しいと思った方は飛ばして次のセクションを見ていただいても大丈夫です。
5.3.1 \theta が小さい方から \frac{\pi}{2} に近づくとき
\theta が \frac{\pi}{2} より少し小さな値、例えば \theta = \frac{\pi}{2} - 0.1 から徐々に \frac{\pi}{2} に近づいていくことを考えましょう。このとき、 Figure 1 を見ると、円周上の点は第一象限から点 (0, r) 、つまり原点の真上の点に近づいていきます。
y は高々 r 程度の値しかとりません。それに対して \theta が \frac{\pi}{2} に近づくと、 x の値は正の値をとりつつも、どんどん 0 に近づいていきます。つまり、どんどん小さな正の値をとります。
例えば、以下のように小さな正の値をとっていくとしましょう:
\frac{1}{10}, \frac{1}{100}, \frac{1}{1000}, \frac{1}{10000}, \cdots
この時、タンジェントの定義 \tan \theta = \frac{y}{x} = t \times \frac{1}{x} において、 \frac{1}{x} の値は、上記の数の上下をひっくり返した値になります:
10, 100, 1000, 10000, \cdots
つまり、 x の値が小さくなる時、タンジェントの定義中の \frac{1}{x} はどんどん大きな値をとります。結果としてタンジェントはどこまでも大きな値をとることができます。
以上のことから、タンジェントはどんな正の値もとることができます。また \tan 0 = 0 ですから、タンジェントは 0 もとります。
5.3.2 \theta が大きい方から \frac{\pi}{2} に近づくとき
逆に \theta が \frac{\pi}{2} + 0.1 のように、 \frac{\pi}{2} よりも大きな値から \frac{\pi}{2} に近づく場合を考えてみましょう。
このとき、先ほどと同様 y は高々 r 程度の値しかとりません。一方、 x は 0 に近づいていきますが、先ほどとは異なり、 x は負の値をとります。つまり、 \frac{1}{x} は、
-10, -100, -1000, -10000, \cdots
のように絶対値は大きくなるものの、負の値とります。したがって、タンジェントはどんどん小さな値 (絶対値は大きくなる) をとり、どこまでも小さな負の値をとることができます。
以上から、タンジェントは任意の実数値をとることが確認できました。
5.4 三角関数の取りうる値の範囲:まとめ
以上のことをまとめると、サインとコサインは -1 以上 1 以下の値、タンジェントは任意の実数値をとります。
6 今後の学習のコツ
三角関数の定義は三角関数の勉強を進めるうえで必須であり、この先何度も利用します。特に、定義を使った代表的な三角関数の値を求める方法に慣れておくことで、定義自体の理解が深まるうえ、三角関数の値を覚えておく必要がありません。定義を使って値を求める練習を進めておきましょう。









