1 三角比
三角関数は三角比を拡張した考え方です。三角比は直角三角形の辺の比と角度を対応させています。Section 2 で説明するように、三角関数は円を使って定義されますが、あくまでも基本は、三角比における直角三角形を使った考え方です。三角関数を学ぶにあたって、簡単に三角比について知っておきましょう。
三角比は Figure 1 に示した直角三角形の角度と辺の比を対応させています。“\sin \theta は \theta と向かい合う辺と斜辺の比”、 “\cos \theta は \theta に隣接する辺と斜辺の比”、そして “\tan \theta は斜辺以外の2辺の比”を表します。

2 三角関数の定義
三角関数は Figure 2 のように円を使って定義されます。
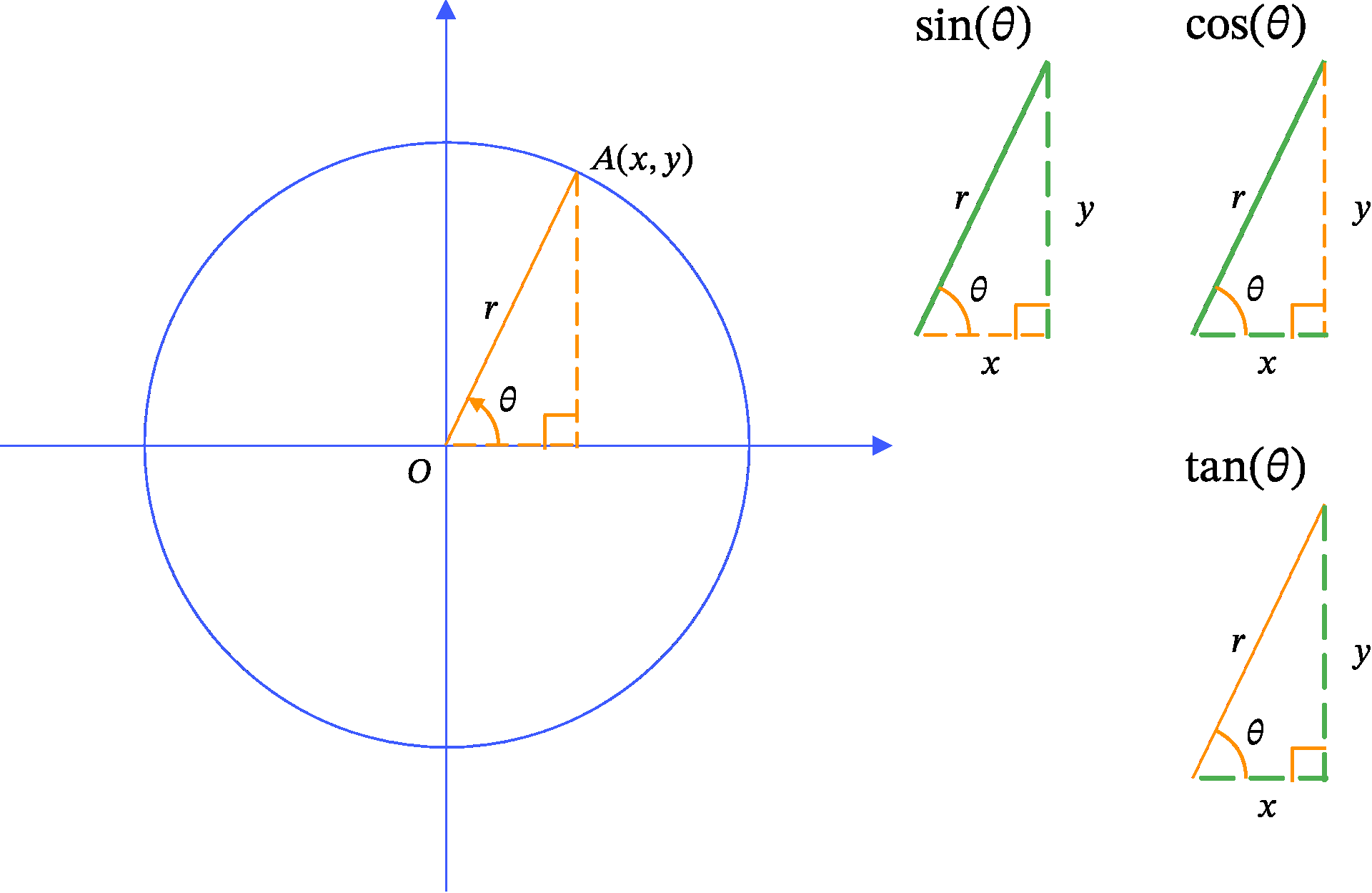
半径 r の円において、x 軸の正の方向から反時計回りに角度 \theta を測り、円周上の点 A(x, y) を描きます。このとき、円の半径 r と点 A の座標 x、y を使って、三角関数は以下のように定義されます。
\begin{aligned} \sin \theta &= \frac{y}{r}\\ \cos \theta &= \frac{x}{r}\\ \tan \theta &= \frac{y}{x} \end{aligned}
3 三角関数と三角比の関係
Figure 1 と Figure 2 を比べると、三角関数を定義する円の中に、三角比を定義する直角三角形が見えます。実際、 0 < \theta < 90^\circ においては、三角比と三角関数が表す値に違いはありません。ところが、三角比はあくまでも直角三角形が存在していることが前提です。例えば \theta = 0^\circ や \theta = 90^\circ では、直角三角形を作ることができず、三角比を定義できません。
三角関数は三角比の考え方を拡張し、直角三角形を前提としていません。代わりに円の半径と円周上の点の座標を用いています。この条件であれば、三角比では扱うことのできなかった角度に対しても、同様の概念を定義することができます。この拡張した概念が三角関数です。
4 度数法と弧度法
三角比では 0^\circ, 45^\circ など、“度” (degree) (単位: ^\circ) という単位をもった角度を使うことが多いです。このような角度を表す方法は度数法と呼ばれ、日常生活でも広く用いられます。
一方の三角関数では、度数法ではなく弧度法と呼ばれる方法で角度を表します。弧度法では”ラジアン” (radian) (単位: rad) という単位で角度を表します。ラジアンは”円の弧の長さ”の、“円の半径”に対する比で定義されます (Definition 1)。
Definition 1 (ラジアンを使った角度の定義) \theta = \frac{l}{r}.
ここで、 l は弧の長さ、 r は円の半径を表す。
Definition 1 では半径 r の円において、点 A(r, 0) から、反時計回りに弧の長さが l となる点 B をとります (Figure 3)。 このとき角度 \theta が Definition 1 によりただ1つに決まります。これがラジアンという単位で表された角度です。

“度”と”ラジアン”の間には、以下の関係が成立します:
360^\circ \Leftrightarrow 2 \pi \tag{1}
5 半径に依存しない三角関数
三角関数は円を使って定義されますが (Figure 2)、 この円の半径には依存せずに値が決まります。言い換えると、どのような半径の円を考えても、 \theta が一定であれば、三角関数は常に同じ値を持ちます。
このことは、三角関数の値を計算する際、値を計算しやすい、適当な半径の円を考えてよいことの根拠になります (Section 6)。
6 三角関数の計算
三角関数の定義 Figure 2 を使って、代表的な三角関数の値を計算することができます。例えば、\theta = \frac{\pi}{3} の時に、三角関数の値を計算してみましょう。
Equation 1 によると、2 \pi と 360^\circ が対応します。\frac{\pi}{3} は 2 \pi に \frac{1}{6} を掛けて得られますので、 360^\circ にも同様に \frac{1}{6} を掛けると、 \frac{\pi}{3} = 60^\circ という関係であることがわかります。
60^\circ をもった直角三角形の辺の比は、1 : 2 : \sqrt{3} であることが知られているので、Figure 4 のように半径 2 の直角三角形を考えるとよさそうです。Section 5 より、半径 2 の円でも直角三角形の値は問題なく計算できます。

後は三角関数の定義 (Figure 2) に従うと、以下のように計算できます:
\begin{aligned} \sin \theta &= \frac{\sqrt{3}}{2},\\ \cos \theta &= \frac{\sqrt{1}}{2},\\ \tan \theta &= \frac{\sqrt{2}}{1} = 2. \end{aligned}
今回は半径 2 の円を使いましたが、\theta = \frac{\pi}{4} などに対しては、直角二等辺三角形を考え、半径 \sqrt{2} の円を考えた方が計算しやすいです。
7 三角関数の公式
三角関数の公式はかなり数が多いですが、定義、または加法定理を使って簡単に証明・導出することができます。各公式の証明方法を理解しておけば、覚えておく必要のある公式の数は、かなり少なくなります。
公式を丸暗記するのではなく、公式の証明を理解して自分で証明できるようになる方が、三角関数自体の理解が深まるうえ、応用力の形成、そして長期的な記憶の定着にも効果的だと思います。
三角関数の公式は、“(1) 三角関数の定義を使って証明されるグループ”と、“(2) 加法定理を使って証明されるグループ”に分類して、証明方法を理解することをお勧めしています。三角関数の公式のまとめについては、以下の記事をご覧ください:
8 三角関数のグラフ
関数について考えるときは、関数のグラフを多用します。三角関数のグラフを学習し、三角関数の特徴についての理解を深めましょう。
8.1 三角関数の周期
Figure 5 に示すように、三角関数のグラフは、周期的な構造をもちます。y = \sin x と y = \cos x は周期 (基本周期) 2 \pi を、y = \tan x は周期 \pi を持ちます。周期とは、関数の y の値を同じ値に到達させる x の変化のことです。より正確には、以下の式を満たす定数 p を、関数 f の周期といいます:
f(x) = f(x + p)
この式は、定義域に含まれるどのような x に対しても、p だけずれると、同じ y の値をとることを意味しています。例えば Figure 5 (a) では、 x = 0 のとき、y = 0 であり、紫色のバーの幅 2 \pi だけずれた x = 2 \pi のときも、 y = 0 となり、同じ y の値をもちます。
x = \pi のときも y = 0 ですが、例えば x = \frac{\pi}{2} (山の頂上)から \pi ずれただけでは、x = \frac{3 \pi}{2} となり、対応する y の値が谷の底を示し、同じ y の値にはなりません。したがって、 \pi は y = \sin x の周期ではありません。
同様に y = \cos x も周期 2 \pi をもち、y = \sin x 同様、上がったり下がったりという波のような周期的な構造をしています。
これに対して y = \tan x の周期は \pi であり、 x = \frac{\pi}{2} や x = - \frac{\pi}{2} では関数自体が定義されていません。

紫色のバー: 周期. 黄色のバー: 振幅
8.2 三角関数の振幅と最大値、最小値
“振幅” (amplitude) は、波の高さの方向における、中心から頂上までの幅を意味します。Figure 5 (a),(b) では、黄色のバーの幅が”振幅”です。波の高さの方向における中心が x 軸に対応します。y = \sin x、y = \cos x ともに、振幅は 1 です。
Figure 5 からわかる通り、実質、振幅は最大値ですので、y = \sin x や y = \cos x の最大値、最小値は、それぞれ 1、 -1 であることがわかります。一方で、y = \tan x は - \infty から \infty まで任意の実数値を持ちます。
8.3 三角関数の定義域、値域
関数は、入力値をただ一つの出力値に対応させる関係のことです。入力値がとりうる値全体からなる集合を”定義域” (domain)、そして出力値がとりうる値全体からなる集合を”値域” (range) と言います。
三角関数では、定義域はとりうる角度全体です。Figure 5 からわかるように、 y = \sin x や y = \cos x では、定義域として実数全体を考えることができます。それに対して、y = \tan x は x = \frac{\pi}{2} + n \pi, n \in \mathbb Z において、定義されません。\mathbb Z は整数全体からなる集合です (Table 1)。
y = \sin x や y = \cos x は -1 から 1 までの値をとりますので、 -1 \le y \le 1 が値域となります。一方 y = \tan x は任意の実数をもつことができ、その値域は - \infty < y < \infty となります (Table 1)。
| 関数 | 定義域 | 値域 |
|---|---|---|
| y = \sin x | -\infty < x < \infty | -1 \le y \le 1 |
| y = \cos x | -\infty < x < \infty | -1 \le y \le 1 |
| y = \tan x | x = \frac{\pi}{2} + n \pi, n \in \mathbb Z を除く任意の実数 | -\infty < y < \infty |
8.4 三角関数と偶関数・奇関数
三角関数の特徴として、偶関数や奇関数であることも挙げられます。簡単に言って、偶関数や奇関数は、以下の条件を満たす関数を言います:
- 偶関数: グラフが y 軸に関して対称である。
- 奇関数: グラフが原点に関して対称である。
Figure 5 に示した通り、y = \sin x のグラフは原点に関して対称 (原点を中心に 180^\circ 回転させると元のグラフに重なる) ですので、奇関数です。同様に y = \tan x も奇関数です。一方の y = \cos x は y 軸に関して対称 (y 軸を折り目にするとグラフが重なる) ですので、偶関数です。
9 三角関数のグラフの平行移動と拡大・縮小
Figure 5 に示したグラフを基本としつつ、これらのグラフを平行移動したり、拡大・縮小したグラフについても、考えることがあります。
9.1 三角関数のグラフの平行移動
一般に、関数 y = f(x) のグラフを x 軸方向へ p、 y 軸方向へ q だけ平行移動したグラフを表す関数は、以下の形で表されます:
y - q = f(x - p).
この関数は、y = f(x) において、x \rightarrow x - p、 y \rightarrow y - q という置き換えにより、得ることができます。
したがって、各三角関数のグラフを x 軸方向へ p、 y 軸方向へ q だけ平行移動したグラフを表す関数は、それぞれ以下のようになります:
\begin{aligned} y &= \sin x \quad \rightarrow \quad y - q = \sin (x - p),\\ y &= \cos x \quad \rightarrow \quad y - q = \cos (x - p),\\ y &= \tan x \quad \rightarrow \quad y - q = \tan (x - p).\\ \end{aligned} \tag{2}
Figure 6 に三角関数のグラフを平行移動したグラフの例を示します。紫色の破線が y = \sin x など、もともとのグラフです。これらのグラフを平行移動したグラフを青色の実線で示しています。
例えば Figure 6 (a) では y = \sin x のグラフを y = \sin \left( x - \frac{\pi}{2} \right) のグラフへと平行移動しました。紫色の丸で示した破線のグラフ上の丸が、実線のグラフ上の青色の丸に移動している点に、注意してください。
Equation 2 と比較すると、この例では y = \sin x のグラフを x 軸に沿って \frac{\pi}{2} だけ平行移動していることがわかります。
Figure 6 (c) では、y = \tan x のグラフを x 軸方向に \frac{\pi}{2}、y 軸方向に 1 平行移動しています。

紫色の破線: y = \sin x, y = \cos x, y = \tan x. 青色の実線: 平行移動した後のグラフ. 平行移動により、破線上の紫色の丸が、実線上の丸へ移動する.
9.2 三角関数のグラフの拡大・縮小
三角関数のグラフは、 y 軸、または x 軸方向に拡大・縮小することができます。例えば以下の式は、y = \cos x のグラフを y 軸の方向に a だけ拡大・縮小することを意味します:
y = a \cos x. \tag{3}
例えば Figure 6 (b) では、 y = \cos x のグラフが、 y 軸に沿って 2 倍に拡大されています。
また、以下の式は、 y = \cos x のグラフを x 軸方向に \frac{1}{b} だけ拡大縮小します:
y = \cos (bx). \tag{4}
つまり、y = \cos (2x) (b=2 のとき)、y = \cos x を x 軸方向に \frac{1}{2} 倍に縮小します。結果として -2 \pi \le x \le 2 \pi の間にある波の山の数が増えることになります (Figure 6 (b))。
9.3 三角関数のグラフの平行移動と拡大・縮小まとめ
Equation 2、 Equation 3、 Equation 4 を合わせると、三角関数のグラフを平行移動、または拡大・縮小する変形全体は、以下の式で表されます (代表して y = \cos x についてのみ記載していますが、他の関数でも同様です):
\begin{aligned} y = \cos x \rightarrow y - q &= a \cos (b(x - p))\\ y &= a \cos (b(x - p)) + q. \end{aligned}
この三角関数のグラフは以下の特徴を持ちます:
- 振幅 (amplitude): \vert a \vert
- 周期 (period): \frac{2 \pi}{\vert b \vert}
- y = \cos x を基準とした x 軸方向への移動 (phase shift): p
- y = \cos x を基準とした y 軸方向への移動 (vertical shift): q
Figure 7 に y = 2 \cos \left(\frac{1}{2} \left(x - \frac{\pi}{2} \right)\right) + 1 のグラフを描いていますので、振幅、周期、x 軸、 y 軸への移動について、それぞれ確認してみてください。

紫色の破線: y = \cos x. 青色の実線: y = 2 \cos \left(\frac{1}{2} \left(x - \frac{\pi}{2} \right)\right) + 1. 破線上の紫色の丸が、実線上の丸へ移動する.
10 まとめ
本記事では、三角関数の基本事項について幅広く解説しました。本記事内のリンクから、より詳しい解説にアクセスできます。特に三角案数の公式については、一通り証明方法を理解しておくことで、覚える内容を、大きく減らすことができます。本記事で学習したことをベースに、三角関数の理解をさらに深めていきましょう。



